Homepage Andreas Schmitt

|
Univ.Ass. Dr. Andreas Schmitt aschmitt at hep.itp dot tuwien dot ac dot at |
Research
Color superconductivity in dense quark matter
Matter at high density and low temperature is expected to be a color superconductor which is a degenerate Fermi gas of quarks with a condensate of Cooper pairs near the Fermi surface that induces color Meissner effects. A review of color superconductivity that I have written together with M. Alford, K.Rajagopal, and T. Schaefer can be found here.
At asymptotically high densities the ground state is the color-flavor locked (CFL) phase which is a particularly symmetric state where all quarks participate in Cooper pairing. CFL is a superfluid, it breaks chiral symmetry, and is an electromagnetic insulator. The densities at which rigorous first-principle calculations from Quantum Chromodynamics (QCD) can be performed are well beyond densities reached for instance in the interior of compact stars.
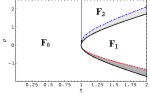
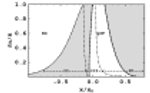
It is an exciting and challenging problem to determine the ground state of deconfined quark matter at more moderate, astrophysically relevant, densities, where QCD calculations become extremely complicated due to the strong-coupling nature of the interaction. In addition, the effect of the strange quark mass, together with electric neutrality and weak equilibirum, induces a mismatch in the Fermi momenta of the quarks that pair in the CFL phase. It is therefore unclear whether CFL persists down to densities where the transition to hadronic matter sets in or whether there are other, less symmetric, color-superconducting phases in between. Some of these candidate phases break rotational and/or translational invariance, possibly exhibiting crystalline structures.
Since QCD becomes unwieldy at the relevant densities, it is important to make use of astrophysical data to rule out or confirm candidate phases. In this context I have written a pedagogical introduction to the physics of compact stars (see also teaching below). This introduction is also available as a book.
One may for instance relate the equation of state of (color-superconducting) quark matter to the mass and radius of a compact star. Another, maybe more promising approach, which enables us to get information about the matter in the interior of a compact star, is to relate the rotation frequencies of the star to shear and bulk viscosity of quark (and nuclear) matter.
The research field of color superconductivity, or more general: dense quark matter and the physics of compact stars, is exciting for several reasons. Firstly, it deals with matter on a fundamental level. In other words, by studying matter under extreme conditions (here: large density) one learns a lot about the underlying fundamental theory (QCD), also for less extreme conditions. Secondly, as exotic as ultra-dense matter may seem, it exists in nature. Although currently no experiment on earth can produce this kind of matter, it is present in the interior of compact stars. Whether this is indeed deconfined quark matter and whether it is indeed a color superconductor, is uncertain. Thirdly, since the field brings together many ingredients from other research fields, interactions to related areas such as condensed matter physics or atomic physics is necessary and fruitful. For instance, systems of cold fermionic atoms in optical traps serve to mimic certain aspects of dense quark matter in exciting experiments in the lab.
QCD at finite temperature and density via the holographic principle
A powerful tool to study strongly-interacting gauge theories is the equivalence of certain string theories in 10 dimensions to corresponding ("dual") field theories living on the boundary of the higher-dimensional space. This "holographic" description has originally been applied to a string theory in Anti-de-Sitter (AdS) space having a supersymmetric conformal field theory (CFT) as its dual ("AdS/CFT correspondence"). Its benefit and great potential lies in the fact that the strong-coupling results of one side can be obtained by performing weak-coupling calculations on the other side. For our purposes this means that the (relatively simple) (super-)gravity approximation on the string theory side provides us with insight into the (very hard) strong-coupling regime of the field theory.
QCD is neither conformal nor supersymmetric, and a dual string theory is currently not known. Therefore, two approaches are possible to gain insight into QCD (or other strongly-coupled field theories). First, one may stick to the original AdS/CFT correspondence and compare the results for instance to heavy-ion collisions which are governed by QCD. Here one relies, despite the big differences, on possible parallels between the conformal field theory and QCD. Second, one may try to improve the original correspondence to find dual field theories with properties closer to QCD, ultimately maybe to find a string theory dual for QCD itself.
On of these "improved" dualities is the Sakai-Sugimoto model. In this model, supersymmetry is completely broken and chiral symmetry breaking as well as confinement is accounted for in a beautiful geometric way. (One is, however, still restricted to the large-N limit, where N is the number of colors which in QCD is 3 and thus not really large.) I am interested in applying this and related models to questions of QCD at finite temperatures and densities. For instance, the interplay of hot and/or dense matter with a magnetic field is interesting and may show spectacular effects, possibly observable in heavy-ion collisions. Also, it is an open question which features of the large-N QCD phase diagram survive for N=3. In particular, is there a "quarkyonic" phase in QCD, as suggested from the case of large N?
Selected presentations
- Sound modes and the two-stream instability in relativistic superfluids (2014)
- Dense matter in a magnetic field - from a field-theoretic and a holographic point of view (lectures, 2013)
- Quark superfluidity in the two-fluid formalism (2012)
- Inverse magnetic catalysis in dense holographic matter (2012)
- Color superconductivity in the QCD phase diagram and in compact stars (2011)
- Stressed Cooper pairing in dense quark matter (2010)
- The chiral magnetic effect in holographic QCD (2010)
- Color superconductivity in dense quark matter (lectures, 2009)
- Bulk viscosity in 2SC quark matter (2006)
- Stressed pairing in conventional color superconductors is unavoidable (2006)
- Neutrino emissivity from spin-1 color superconductors (2005)
Teaching
Introduction to superfluidity - Field-theoretical approach and applications, WS 2014/15
Mondays 12:15 - 13:45, Seminar room E136, 10th floor, First Meeting: October 6th, 2014
NO LECTURE on October 27, 2014!
ADDITIONAL LECTURE on January 15, 2015, 12:30, Seminar room E136!
Superfluidity and superconductivity are very general phenomena. Their underlying mechanisms can occur on vastly different energy scales and thus apply to various different areas of physics. I will introduce the basic theoretical concepts of bosonic and fermionic superfluidity/superconductivity as well as the hydrodynamics of superfluidity in relativistic and non-relativistic contexts. Besides "usual" superfluids such as liquid helium I will also discuss more exotic ones in atomic and high-energy physics.
Lecture notes (PDF)
- A. Schmitt, "Introduction to superfluidity - Field-theoretical approach and applications"
- List of typos in lecture notes
The Physics of Compact Stars, SS 2014
NOTICE NEW TIME AND LOCATION:
Mondays 13:15 - 14:45, Seminar room 138C, 9th floor (yellow section)
First Meeting: March 3, 2014
NO LECTURE on March 24, 2014!
ADDITIONAL LECTURE on May 9, 2014, 14:15, in Seminar room 138A, 7th floor (yellow section)
Lecture notes
- A. Schmitt, "Dense matter in compact stars - A pedagogical introduction"
- List of typos in lecture notes
Literature
- N.K. Glendenning, "Compact Stars: Nuclear Physics, Particle Physics, and General Relativity", Springer, 2000
- P. Haensel, A.Y. Potekhin, D.G. Yakovlev, "Neutron Stars", Springer, 2007
- D. Page, S. Reddy, "Dense Matter in Compact Stars: Theoretical Developments and Observational Constraints"
Thermal Field Theory WS 2013/14
Mondays 12:15 - 13:45, Seminar room 136, 10th floor (yellow section)
First Meeting: Monday, October 7th, 12:15
NO LECTURE on November 25, 2013!
Lecture notes (PDF)
Literature
- J.I. Kapusta, C. Gale, "Finite-temperature field theory: Principles and Applications" (Cambridge Univ. Press, New York, 2006);
- M. Le Bellac, "Thermal Field Theory" (Cambridge Univ. Press, Cambridge, 2000);
- M. Laine, "Thermal Field Theory" (lecture notes)
- A. Fetter, J.D. Walecka, "Quantum Theory of Many-Particle Systems" (McGraw Hill, New York, 1971).