
Condensed Matter
Phase transitions in soft matter
Soft matter physics has become a rapidly developing branch in condensed matter physics. This is certainly due to the fact that soft matter does play an important role not only in our daily life, but also in many technological applications.
Despite the fundamental role that soft matter plays in our lives, systematic investigations of its properties have been out of reach over many decades which is due to the intrinsic complexity of these systems. Only in recent years special experimental techniques in combination with new theoretical concepts have brought along - in a fruitful cooperation among soft condensed matter scientists - a deeper insight into the intriguing phenomena of these systems. Since typical soft matter particles are mesoscopic in size, they can be be investigated with experimental methods that are much simpler to handle than, for atomic systems: information is obtained directly in real space and particles can be moved in space nearly arbitrarily with optical squeezers.
During the past year we have in particular focused on ionic microgels. They are mesoscopically sized, covalently cross-linked polymer networks, their diameter s being in the range between 10 nm and 1 mm. Most microgels are based on poly(N-isopropylacrylamide) (PNIPAM) or related co-polymers that are cross-linked during emulsion polymerization, a process that can produce remarkably uniform particles. When the polymer chains comprising the microgels carry ionic groups on their backbones, the latter dissociate upon solution into an aqueous solvent, leading to charged or ionic microgels. Active interest in polyelectrolyte gels (to which microgels belong as a subgroup) remains to date, due to their ability to absorb large amounts of water and act as superabsorbers or drug delivery systems.
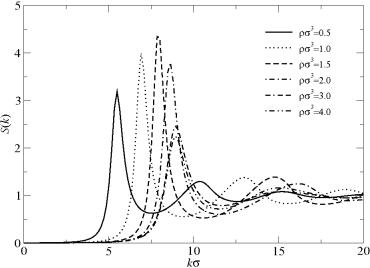
Fig.: Anomalous behaviour of the structure factor S(k) for microgels with charge Z = 250 and size =100 nm for increasing density.
Phase behaviour and criticality in simple liquids and their mixtures
Liquid state theories establish a link between the microscopic properties of a liquid (in terms of its pair potential) and its structural and thermodynamic properties. Statistical Mechanics provides the versatile formalism to determine the relevant relations. In practice, however, these expressions cannot be applied directly, not even for the simplest non-ideal system, i.e., to hard spheres: the reason is that they become intractably complex and therefore require simplifying assumptions. These simplifications lead to approximate schemes that can be derived systematically (e.g., via graph-theoretical considerations) from the exact expressions for partition sums and related quantities. One thus arrives at so-called closure relations to the Ornstein-Zernike equation that relate the total and the direct correlation functions which describe the structural properties of the system. In early years of liquid state theory well-known conventional schemes, such as the mean spherical approximation (MSA), the Percus-Yevick (PY), or the hypernetted chain (HNC) approximations have been derived.
In recent time we have successfully extended the Self-Consistent Ornstein-Zernike Approximation (SCOZA) to a large variety of systems: for liquids with repulsive core (as they are, e.g., encountered in atomic systems) we are now able to consider potentials with arbitrary attractive tails. Comparison with computer simulations has shown that SCOZA does indeed remain accurate close to phase boundaries and in the critical region. Particular attention has recently been dedicated to soft systems, i.e., liquids where the potential of the particles remains finite at the origin or diverges only weakly for short distances; such interactions are typical for soft matter particles. Also here we could show that computer simulation data for the structural and thermodynamic properties could be reproduced with high accuracy.
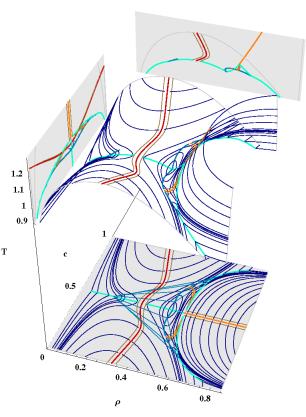
Fig.: Three dimensional representation of the phase diagram of a binary symmetric mixture for = 0, 69.
Special emphasis has furthermore been put on closer investigations of the HRT scheme. It is in particular the implementation of HRT which represents a challenge (both from the conceptual as well as from the numerical point of view). In an effort to localize the phase boundaries and the critical point with high accuracy, states of diverging compressibility have to be identified which turned out to be a very delicate problem.
Interaction of slow highly charged ions with solid surfaces
The study of multiply-charged ion-solid interactions is of considerable technological importance for the understanding of material damage, surface modification, and plasma-wall interactions. The recent availability of sources for slow highly charged ions (HCI), namely electron cyclotron resonance (ECR) and electron beam ion sources (EBIS) has led to a flurry of research activities, both experimental and theoretical, in the field of HCI-solid interactions. On the most fundamental level, its importance is derived from the complex many-body response of surface electrons to the strong Coulomb perturbation.
From numerous experimental as well as theoretical studies the following scenario of the HCI-surface interaction has emerged: When an HCI approaches a solid surface, one or more electrons are resonantly captured at large distances into high Rydberg states of the projectile. As a result, so-called hollow atoms (ions) are formed where the atomic charge cloud transiently resides in shells with large diameters while the core is virtually empty. Direct observation of this short-lived state is complicated by the fact that the ion is always attracted towards the surface by its self-image potential. Consequently it will suffer close collisions upon impact on the surface and the memory of the hollow atom is all but erased. This problem has motivated the study of interactions of HCI with internal surfaces of microcapillaries and nanocapillaries as an alternative technique to study above surface processes.
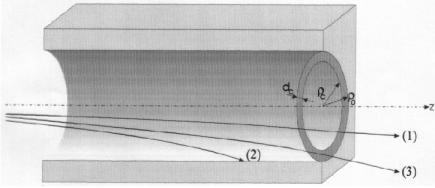
Fig.: Schematic picture of a capillary and three types of trajectories.
Metal and insulating capillaries have become available at the Tokyo Metropolitan University, Japan, and at the Hahn-Meitner-Institut Berlin, Germany. The use of capillary targets allows the extraction of hollow atoms in vacuum. Observation of photons or Auger electrons emitted from them in flight becomes possible. Also the energy loss an HCI suffers when passing through a capillary at distances too large for charge transfer to take place can be measured and calculated.
Theoretical and computational condensed matter physics
Computer simulations using quantum mechanical many-electron theories to solve the Schrödinger equation can be used to study ground- and excited state properties of real materials. This research field is highly interdisciplinary and situated at the crossroads of theoretical condensed matter physics, computational materials physics and theoretical quantum chemistry. More information can be found at: http://cqc.itp.tuwien.ac.at/ and these presentation slides
