Physics of Complex Systems
Rydberg molecules
Rydberg atoms are true giants in the atomic world with sizes reaching 10 micrometer for n=300 and constitute mesoscopic entities. They allow to probe classical-quantum correspondence and the transition from the quantum to the classical world. They also provide a useful testing ground for concepts of non-linear dynamics since even moderate external (magnetic or electric) fields provide strong non-separable perturbations. Rydberg atoms have recently attracted attention also in the quest for building blocks of quantum information systems. Rydberg atoms have been proposed as a quantum phase register and as quantum gates employing the Rydberg dipole blockade. The latter makes use of the strong long-range dipole-dipole interactions which conditionally block excitations of atoms in the vicinity of a Rydberg atom already created. More generally, an ensemble of ultracold Rydberg atoms constitutes a strongly interacting many-body system far from the ground state.
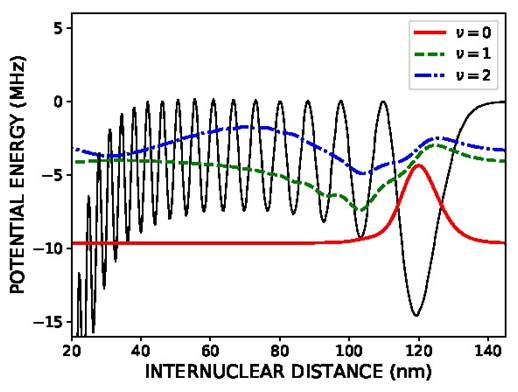
Rydberg molecules are another interesting topic which can, for example, be used as a sensitive probe for the spatial distribution of ultracold gases. When a Rydberg atom is excited in a dense gas of atoms, one or more ground-state atom(s) can be found within the Rydberg electron orbit. For an attractive interaction between the quasi-free Rydberg electron and a ground-state atom an ultralong-range Rydberg molecule can be formed. Typically the interaction and the resulting binding energy are very small and a low kinetic energy of a ground state atom is required and the formation of Rydberg molecules is observed in an ultracold gas of atoms (of the order of 1 μK or less). Within the Born-Oppenheimer approximation, the molecular potential experienced by a ground state atom is approximately proportional to the squared wave function of Rydberg electron. This is because the interaction is larger at higher probability density of Rydberg electron (Fig.1). The vibrational levels are formed by trapping a ground state atom within these potential wells.
Fig.1 : Molecular potential (black line) for a 5s38s 3S1 strontium atom together with the wavefunctions for the v = 0 (red solid line), v = 1 (green dashed line), and v = 2 (blue dot-dashed line) molecular vibrational states. The binding energy corresponding to each wave function is indicated by its axis.
For a Rydberg dimer the lowest energy vibrational state has a wavefunction well localized in space around Rn = 2 n2 (a.u.) (Fig.1). Thus, the probability of creating the dimer molecule will depend on the likelihood of initially finding a pair of ground-state atoms with the appropriate internuclear separation, Rn. By varying the principal quantum number of the Rydberg atom the wavefunction can be localized at different positions and a pair distribution at different distances can be probed. For example, the excitation of Rydberg dimers between n=30 and 50 leads to a pair correlation in the range of R = 90nm and 250nm. This technique has been applied to an ultracold gas of bosons as well as fermions and the exchange hole in the two-body correlation of a fermion gas has been observed.
The Rydberg molecule can also be extended to involve more than one ground-state atom. An excitation of Rydberg trimer in which two ground-state atoms are bound may open a possibility to probe a three-body correlation of ultracold gases. By increasing the density of a gas or the principal quantum number n, the number of ground state atoms within a Rydberg molecule can be increased. Currently, a Rydberg molecule involving up to about 10000 atoms has been created.
For more information about this topic, please consult the following websites: http://dollywood.itp.tuwien.ac.at/~shuhei/ https://tqd.itp.tuwien.ac.at/
Ultrashort pulses
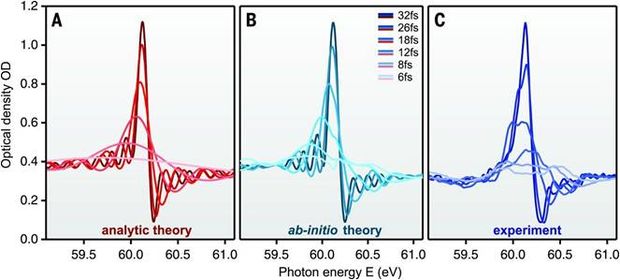
Ultrashort pulses as first characterized at TU Wien are the ultimate tool to investigate the fundamentals of light-matter interactions and the meaning of time and time differences in quantum mechanics. We have studied, e.g., the full two-electron dynamics of helium atoms irradiated by strong and short laser pulses to calculate the apparent time delay of photoemission from different initial states of the parent atom (together with MPQ Garching, TU Munich). To this end, we have solved the two-electron Schrödinger equation for helium and have successfully simulated so-called attosecond streaking and RABBITT experiments both of which measure the relative time delay of different electron groups reaching the detector. Our simulation results are used to determine time delays on an absolute scale and have allowed for a detailed look into photon-induced excitation processes in atoms. Our simulation results were also used to work out the time evolution of the temporal build-up of interference structures in photoemission (Fano resonances, MPI Heidelberg). These interferences are caused by two alternative pathways to the same final state, e.g., direct emission vs. delayed emission via a metastable excited state. Pump-probe experiments with variable delay between the two pulses interrupt the build-up of the resonance and allow for taking snapshots of the process thereby showing the temporal evolution of the multipath interference.
Fig. 2: Temporal build-up of a two-path interference in the photoionization of helium. Results of our simulations are compared to experimental data. Asymptotically, the energy spectrum converges to the well-known Fano shape.
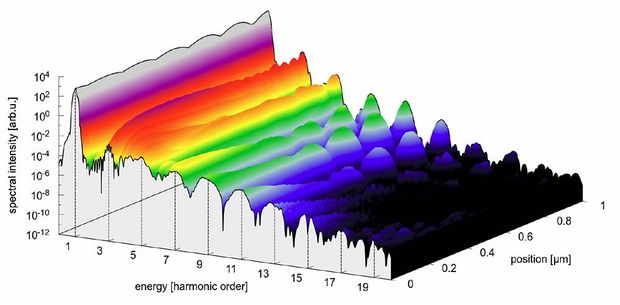
Another interesting application of attosecond science is the non-linear upconversion of photons of a strong incident laser pulse to high-order multiples of the original photon energy in a process called high-harmonics generation. Recently, upconversion factors of more than 1000 could be reached at TU Wien (Institute for Photonics) in this process. Our work helps to interpret the experimental results and to optimize this process aimed at generating XUV pulses of sub-as duration. Lately, attosecond experiments have also been performed on extended systems such as dielectrics, where the high target-atom density raises hopes to generate harmonics with larger intensity. Due to the inherent multi-particle nature of such systems, simplified models have been invoked that have given first qualitative insight in the light-driven electronic processes in dielectrics. However, we could show that such simplifications often fail to reproduce even the qualitative behavior of realistic systems let alone provide a quantitative prediction for any observable in experiment. We have taken the first steps to a multi-scale description of laser-solid interactions combining the microscopic electronic motion described by the Schödinger equation with the mesoscopic world of light propagation (Maxwell's equations).
Fig. 3: High harmonic spectrum induced in diamond by a linearly polarized few-cycle laser pulse as a function of the position along the propagation direction inside a 1 µm thick diamond crystal.
Working together with experimental groups in Munich, Zurich, and Graz we have elucidated the interplay of different processes involved in light-solid and light-liquid interactions and have helped interpret fundamental experiments in the field possibly paving the way to light-driven electronics on the PHz scale.
For more information about this topic, please consult the following websites: http://concord.itp.tuwien.ac.at/~lemell/ https://tqd.itp.tuwien.ac.at/
Dynamics of many-body systems
Quantum many-body systems are at the core of current interest both in experimental as well as in theoretical physics, since a better understanding of these systems bears a large potential for technology and applications. Table-top sources of coherent X-ray light from strongly driven gases of atoms might become available in near future. Highly accurate gravimeters are being constructed using the coherence of matter waves. Petahertz electronics is at reach based on the driving of currents in dielectrics by femtosecond laser pulses. All these applications share that the underlying effects originate from or exploit non-equilibrium quantum matter. Many novel experimental tools are being developed that allow for unprecedented driving for example by strong and ultrashort laser pulses, by bichromatic fields, or by structured light, and are being used to explore new effects and applications.
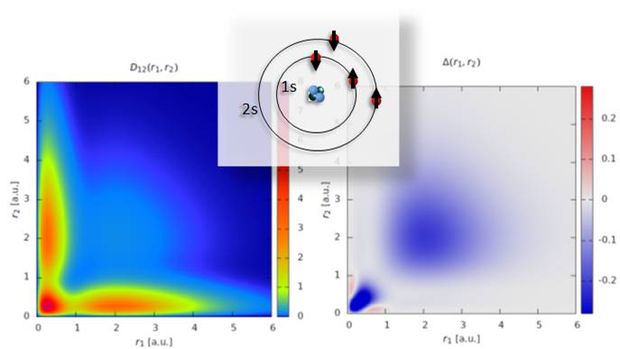
Fig.4: The two-particle reduced density matrix (left) and the cumulant measuring two-particle correlations (right) of the beryllium atom.
At the same time, theoretical tools to describe these systems are lagging behind those available for systems at rest. In our research, we address exactly this discrepancy. We use and develop novel theoretical approaches to describe quantum systems out of equilibrium. Starting point of our investigations into non-equilibrium quantum matter is the many-body time-dependent Schrödinger equation. The complexity of this equation increases exponentially with the number of particles in the system. It thus cannot be solved numerically exactly except for the simplest systems consisting of just a few particles. A simple estimate shows that storing the wavefunction of, e.g. , the lithium atom with reasonable resolution would exceed the storage capacity of current supercomputers not to mention performing calculations with it. One way around is to avoid the wave function and use a reduced object such as the particle density. The time-dependent density functional theory, e.g., follows these lines by using the particle density as the fundamental object. However, it suffers from unknown energy functionals because quantum correlations cannot be easily taken into account. We have developed a time-dependent quantum many-body approach that uses the two-particle reduced density matrix instead. In this way all two-particle correlations are incorporated. Since all fundamental interactions can be regarded as pairwise interactions, two-body correlations are the most important ones. With the new method, we were able to solve a wide variety of problems ranging from the multi-electron dynamics of atoms driven by strong and ultrashort pulses to quench dynamics of ultracold atoms in optical lattices.
For more information about this topic, please consult the following website: https://tqd.itp.tuwien.ac.at/
Quantum transport through nanostructures
Novel nanomaterials and their heterostructures play a central role in current computational material science research. Recent experimental progress has seen an appearance of several two-dimensional solids with a wide range of electronic properties, ranging from the famous semi-metal graphene to strongly insulating hexagonal boron nitride. Modern synthesis techniques for the creation and manipulation of stable layers of two-dimensional crystals have now become well developed. Likewise, noble metal nanoclusters feature high catalytic reactivity and sharp plasmonic resonances that can be tailored to specific energies. By depositing and subsequent transfers, individual layers may be combined like a sandwich, stacking layers in a predefined sequence. The resulting van der Waals heterostructures exhibit interesting new effects that go beyond the physics accessible only by a single layer. Nanostructure devices composed of such components promise a wide range of applications, from highly efficient catalysts or solar cells to ultra-low-power nanoelectronics.
Our research focuses on simulating new nanostructure materials composing realistic nanodevices, including defects and impurities. The term nanodevice in this context refers to the typical device size, up to a few micrometers and containing millions of atoms, but still below mesoscopic dimensions. Consequently, quantum effects play an important role. The theoretical description of these systems thus poses a challenging multi-scale problem, requiring active method development. We simulate transport through nanodevices built by our experimental collaborators (for example at RWTH Aachen or ETH Zürich) as well as the electronic structure and properties of low-dimensional materials and their heterostructures.
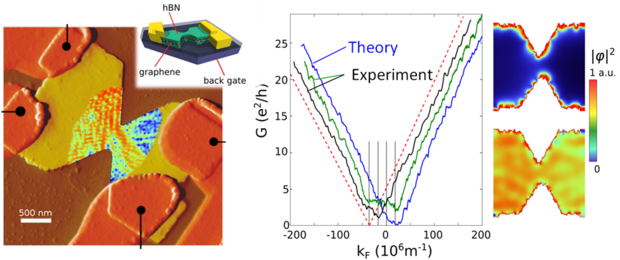
Fig. 5: (left panel) Graphene nano-constriction sandwich device fabricated by the Stampfer group at RWTH Aachen, superposed with the image of a scattering state calculated using our tight-binding approach. Scale bar is 500 nm. (Middle panel) Conductance measurements for two different cool-downs (green and black) and our theory (blue). (Right panel) Local density of states in a graphene nano-constriction for energies close (upper panel) and far away (lower panel) from the Fermi energy.
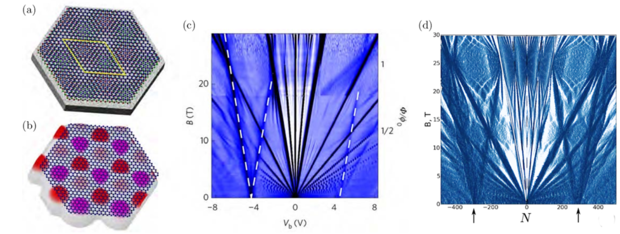
Fig. 6: (a) Hexagonal graphene flake on single hBN layer (carbon: blue, nitrogen: green, boron: red) and substrate. The lattice mismatch generates a moiré pattern with unit length depending on the angle of rotation between the two layers (yellow diamond). (b) Graphene flake in an effective embedding potential which replaces hBN and the substrate - the system size is strongly reduced. (c,d) Density of states of graphene on hexagonal boron nitride, as a function of magnetic field for (c) experiment [Yu 2014] and (d) our theoretical simulations. Notice the linear structures (dashed lines) above and below the Dirac point that emerge due to superlattice effects.
A small lattice mismatch between adjacent layers, for example for graphene and hexagonal boron nitride, gives rise to regular, periodic moiré patterns [see Fig. 6(a)]. Even in structures composed of layers of the same material, twisting the layers with respect to each other will induce moiré potentials, whose periodicity sensitively depends on the twist angle. The resulting heterostructures feature altered electronic properties such as unconventional superconductivity or Mott-insulating phases. From a broader scope, twist angles allow for modifying the band structure of the heterostructure in surprising ways, promising a pathway towards engineering of desired material properties. Unfortunately, theoretical treatment of the large unit cells of moiré patterns, including a substrate and adjacent functional layers makes a full ab-initio treatment challenging. In an ongoing collaboration with Allan McDonald (Houston, TX, USA), we are developing moiré potentials for twisted trilayer graphene as well as transition metal dichalcogenides. Using an effective moiré potential [see Fig. 6(b)], we can reproduce the observed fine structures resulting from the moiré, see Fig. 6(c,d). Using a quantum dot induced by an STM tip, our experimental collaborators at RWTH Aachen were also able to directly probe moiré potentials, which compared well to our simulations.
For more information about this topic, please consult the following websites: http://dollywood.itp.tuwien.ac.at/~florian/ https://tqd.itp.tuwien.ac.at/
Non-Hermitian physics and complex scattering
The propagation of waves is a topic spanning many spatial and temporal scales, from the fundamental quantum aspects of light-matter interaction to the scattering of radio waves in complex media like the earth’s atmosphere. On all these levels the input from theoretical physics is essential for understanding and controlling such wave phenomena. At the institute, considerable effort is being dedicated to two specific topics in the vast field of wave physics: (i) the non-Hermitian physics associated with waves in systems that are subject to both amplification (gain) and dissipation (loss) as well as (ii) the scattering of waves in disordered media. In both of these research areas, we collaborate strongly with various experimental teams; to come as closely as possible to the situation encountered in the laboratory, we employ numerical techniques and run simulations on the Vienna Scientific Cluster. In the field of non-Hermitian physics (i), we are especially interested in controlling the scattering properties of systems by tailoring the spatial distribution of gain and loss in them. Using such an approach, we found, e.g., that a highly disordered system can be made completely transparent and even invisible by adding a tailored gain/loss distribution to it [see Fig. 7(a) for the case of a Gaussian laser beam]. Special attention also receives a particular non-Hermitian singularity, called an exceptional point, that leads to quite a number of fascinating phenomena that we could recently demonstrate in collaboration with different experimental groups in nano-photonics and in laser physics.
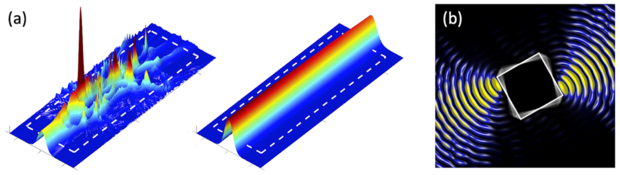
Fig. 7: (a) A Gaussian laser beam entering a disordered medium from the left gets scattered and builds up a highly complicated interference pattern (left panel). By adding a tailored distribution of gain and loss to this medium, the beam can propagate like in free space (right panel). (b) A specially designed laser beam that applies a well-defined torque onto the quadratic target in the middle, turning it in clockwise direction.
In the field of complex scattering (ii) we are pursuing the challenging goal of controlling how light propagates through disordered media. (Think here of the speckle patterns arising when directing a laser beam at a piece of paper.) How to deal with the complex interferences arising in this context is a challenging question arising in many fields of physics—from biomedical optics to observational astronomy. What comes to our advantage here is the fact that scattering is a deterministic process—at least for classical waves—such that the shape of an incident wave front determines how the wave will propagate through a medium. This insight forms the basis for a series of modern experiments that use spatial light modulators to characterize and to control light fields even in strongly disordered media. Our contributions to this newly emerging field of wave front shaping include, e.g., a concept to generate waves that follow a specific path across a disordered medium or that focus onto a designated point inside of it. Moreover, we also showed how to design waves in order to micro-manipulate a target embedded inside a disordered environment [see Fig. 7(b) for an example]. By tuning the incident wave front we could recently achieve the first realization of a random anti-laser, i.e. the time-reverse of a random laser in the sense that a random medium was shown to perfectly absorb a suitably engineered incoming wave front.
For more information about this topic, please consult the following website: https://rottergroup.itp.tuwien.ac.at