Difference between revisions of "Myon g-2"
| (50 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
Mittlerweile konnte das magnetische Moment des Elektrons (genauer, der g-Faktor) mit einer Genauigkeit von besser als 1:10<sup>12</sup> vermessen werden und parallel dazu die Genauigkeit der theoretischen Vorhersage ebenso auf 12 Stellen nach dem Komma gesteigert werden. Die Übereinstimmung von Theorie und Experiment stellt einen der größten Triumphe der modernen Physik dar. |
Mittlerweile konnte das magnetische Moment des Elektrons (genauer, der g-Faktor) mit einer Genauigkeit von besser als 1:10<sup>12</sup> vermessen werden und parallel dazu die Genauigkeit der theoretischen Vorhersage ebenso auf 12 Stellen nach dem Komma gesteigert werden. Die Übereinstimmung von Theorie und Experiment stellt einen der größten Triumphe der modernen Physik dar. |
||
| − | In den enorm aufwändigen Rechnungen dazu, die Jahrzehnte in Anspruch genommen haben, müssen unter anderem Prozesse berücksichtigt werden, bei denen virtuelle Photonen an anderen virtuellen Photonen gestreut werden. Eine solche Streuung von Licht an Licht ist ein rein quantenfeldtheoretischer Effekt, der weder in der klassischen Elektrodynamik noch in “gewöhnlicher” Quantenmechanik möglich ist. Direkt konnte die Licht-an-Licht-Streuung erst vor |
+ | In den enorm aufwändigen Rechnungen dazu, die Jahrzehnte in Anspruch genommen haben, müssen unter anderem Prozesse berücksichtigt werden, bei denen virtuelle Photonen an anderen virtuellen Photonen gestreut werden. Eine solche Streuung von Licht an Licht ist ein rein quantenfeldtheoretischer Effekt, der weder in der klassischen Elektrodynamik noch in “gewöhnlicher” Quantenmechanik möglich ist. Direkt konnte die Licht-an-Licht-Streuung erst vor ein paar Jahren im Zusammenhang mit Schwerionenkollisionen [https://cerncourier.com/a/atlas-spots-light-by-light-scattering/ am CERN beobachtet] werden, aber indirekt war sie schon längst durch die Übereinstimmung von Theorie und Experiment beim anomalen magnetischen Moment des Elektrons nachgewiesen worden – als ein quantenfeldtheoretischer Effekt unter vielen. Diese virtuellen Prozesse involvieren nicht nur Photonen, Elektronen und Positronen, sondern im Prinzip alle Elementarteilchen, die es überhaupt gibt - allerdings mit umso kleineren Effekten, je schwerer sie sind, denn umso kurzlebiger sind sie als virtuelle Teilchen. |
| + | [[image:Lbl.jpg|150px]] [[image:Lblg-2.jpg|200px]] <br /> |
||
| ⚫ | Beim Elektron kommt man allerdings erst nach der 12. Stelle hinter dem Komma in den Bereich, wo eventuelle Physik jenseits des gegenwärtigen Standardmodells eine Rolle spielen könnte, und bislang gibt es eine nahezu perfekte Übereinstimmung von herkömmlicher Theorie und Experiment (mit einer leichten interessanten Diskrepanz, die das Ziel weiterer verfeinerter Experimente ist). |
||
| + | <small>Links: Licht-an-Licht-Streuung von reellen Photonen (Wellenlinien) durch eine Schleife in der Raumzeit, die von virtuellen Elektronen (Linien mit Pfeil) gebildet wird.<br> Rechts: Licht-an-Licht-Streuung in der Wechselwirkung eines reellen Photons mit einem reellen geladenen Teilchen (unterste Linie) modifiziert dessen magnetisches Moment</small> |
||
| ⚫ | Beim Elektron kommt man allerdings erst nach der 12. Stelle hinter dem Komma in den Bereich, wo eventuelle Physik jenseits des gegenwärtigen Standardmodells eine Rolle spielen könnte, und bislang gibt es eine [https://www.mdpi.com/2218-2004/7/1/28/htm nahezu perfekte Übereinstimmung] von herkömmlicher Theorie und Experiment (mit einer leichten interessanten Diskrepanz, die das Ziel weiterer verfeinerter Experimente ist). |
||
| ⚫ | Ein anderes Elementarteilchen, dessen magnetisches Moment mit ähnlichem Aufwand studiert wurde, ist das Myon. Myonen sind Elementarteilchen, die Elektronen in jeder Hinsicht ähneln, aber etwa 200mal schwerer sind. Ihr anomales magnetisches Moment ist dadurch um einiges sensitiver auf Prozesse mit schweren virtuellen Teilchen. Allerdings ist ihr magnetisches Moment weit schwieriger zu messen, weil Myonen nur einige Mikrosekunden Lebensdauer haben und in Elektronen und Neutrinos zerfallen. Das beste experimentelle Resultat bislang wurde Anfang der 2000er-Jahre in einem Speicherring für Myonen am Brookhaven National Lab (BNL) erzielt, mit dem aufsehenerregenden Ergebnis, dass Theorie und Experiment “schon” in der 9. Stelle nach dem Komma abweichen, mit einer Diskrepanz, die 3.7 Standardabweichungen entspricht. |
||
| + | |||
| ⚫ | Ein anderes Elementarteilchen, dessen magnetisches Moment mit ähnlichem Aufwand studiert wurde, ist das Myon. Myonen sind Elementarteilchen, die Elektronen in jeder Hinsicht ähneln, aber etwa 200mal schwerer sind. Ihr anomales magnetisches Moment ist dadurch um einiges sensitiver auf Prozesse mit schweren virtuellen Teilchen. Allerdings ist ihr magnetisches Moment weit schwieriger zu messen, weil Myonen nur einige Mikrosekunden Lebensdauer haben und in Elektronen und Neutrinos zerfallen. Das beste experimentelle Resultat bislang wurde Anfang der 2000er-Jahre in einem Speicherring für Myonen am [https://www.bnl.gov/physics/ Brookhaven National Lab (BNL)] erzielt, mit dem aufsehenerregenden Ergebnis, dass Theorie und Experiment “schon” in der 9. Stelle nach dem Komma abweichen, mit einer Diskrepanz, die 3.7 Standardabweichungen entspricht. |
||
| + | |||
| + | [[image:Ringmagnet.jpg|400px]]<br /> |
||
| + | <small>BNL-Experiment mit supraleitendem Ringmagnet (blau) © BNL, https://www.g-2.bnl.gov/pictures/index.html</small> |
||
<h2>Das neue Experiment am FERMILAB und neuere theoretische Entwicklungen</h2> |
<h2>Das neue Experiment am FERMILAB und neuere theoretische Entwicklungen</h2> |
||
| Line 23: | Line 29: | ||
Am 7. April 2021 werden die ersten Ergebnisse dazu der Öffentlichkeit präsentiert. Falls schon in etwa die Genauigkeit des BNL-Resultats erreicht oder sogar übertroffen wurde, lässt sich endlich mehr dazu sagen, ob das anomale magnetische Moment des Myons Beiträge von „Neuer Physik“, jenseits des Standardmodells aufweist. Dazu muss natürlich auch die theoretische Vorhersage des Standardmodells eine mindestens so hohe Präzision garantieren können. |
Am 7. April 2021 werden die ersten Ergebnisse dazu der Öffentlichkeit präsentiert. Falls schon in etwa die Genauigkeit des BNL-Resultats erreicht oder sogar übertroffen wurde, lässt sich endlich mehr dazu sagen, ob das anomale magnetische Moment des Myons Beiträge von „Neuer Physik“, jenseits des Standardmodells aufweist. Dazu muss natürlich auch die theoretische Vorhersage des Standardmodells eine mindestens so hohe Präzision garantieren können. |
||
| − | In den letzten zwei Jahrzehnten haben |
+ | In den letzten zwei Jahrzehnten haben mehr als hundert theoretische Physiker daran gearbeitet, die theoretischen Ergebnisse zu verbessern. Zwei physikalische Phänomene, die es zu berücksichtigen gab, bildeten dabei die hauptsächliche Schwierigkeit, deren Präzision zu verbessern. Bei beiden geht es um die Wechselwirkung von virtuellen Photonen mit stark selbst-wechselwirkenden Elementarteilchen, den sogenannten Hadronen, die als Quantenfluktuationen im Vakuum präsent sind. Myonen spüren wegen ihrer größeren Masse deren Effekte viel stärker als die leichten Elektronen. |
Der größere der beiden Effekte ist die hadronische Vakuumpolarisation, die über Beschleunigerexperimente indirekt vermessen werden kann und deren Präzision über die Jahre beständig gesteigert wurde. |
Der größere der beiden Effekte ist die hadronische Vakuumpolarisation, die über Beschleunigerexperimente indirekt vermessen werden kann und deren Präzision über die Jahre beständig gesteigert wurde. |
||
Ein weit kleinerer, aber mit größeren Unsicherheiten behafteter Effekt ist die hadronische Licht-an-Licht-Streuung, bei der vier virtuelle Photonen zusammenkommen. Der Hauptbeitrag dazu ist ein Prozess, der selbst eine Anomalie darstellt: der Zerfall eines neutralen Pions (π<sup>0</sup>) in zwei Photonen bzw. die Produktion eines Pions über zwei Photonen. Diesen Prozess dürfte es in der beobachteten Stärke aus Symmetriegründen eigentlich nicht geben. Quantenfluktuationen können aber Symmetrien aufbrechen, in diesem Fall die sogenannte chirale Symmetrie, die rechts- und linkshändige Quarks gegengleich „rotiert“. Für die Wechselwirkung dieser Pionen mit virtuellen Photonen gibt es zumindest teilweise experimentelle Daten, die für die notwendigen Rechnungen aber extrapoliert werden müssen, und dafür wurden immer stärker verfeinerte Modelle entwickelt. |
Ein weit kleinerer, aber mit größeren Unsicherheiten behafteter Effekt ist die hadronische Licht-an-Licht-Streuung, bei der vier virtuelle Photonen zusammenkommen. Der Hauptbeitrag dazu ist ein Prozess, der selbst eine Anomalie darstellt: der Zerfall eines neutralen Pions (π<sup>0</sup>) in zwei Photonen bzw. die Produktion eines Pions über zwei Photonen. Diesen Prozess dürfte es in der beobachteten Stärke aus Symmetriegründen eigentlich nicht geben. Quantenfluktuationen können aber Symmetrien aufbrechen, in diesem Fall die sogenannte chirale Symmetrie, die rechts- und linkshändige Quarks gegengleich „rotiert“. Für die Wechselwirkung dieser Pionen mit virtuellen Photonen gibt es zumindest teilweise experimentelle Daten, die für die notwendigen Rechnungen aber extrapoliert werden müssen, und dafür wurden immer stärker verfeinerte Modelle entwickelt. |
||
| + | |||
| + | [[image:HLbL.jpg|200px]]<br /> |
||
| + | <small>Licht-an-Licht-Streuung an Quantenfluktuationen mit stark wechselwirkenden Quarks und Gluonen und von ihnen gebildeten Elementarteilchen.</small> |
||
| + | |||
| + | [[image:PionEtcLbL.jpg|200px]]<br /> |
||
| + | <small>Hauptbeitrag dabei ist die Erzeugung und der Zerfall eines virtuellen Pions (π<sup>0</sup>) und ähnlicher (sog. pseudoskalarer) Teilchen (η, η'), die durch die chirale Quantenanomalie bestimmt werden. Letztere führt aber auch zu einem verstärkten Beitrag von sogenannten Axialvektorrmesonen (a<sub>1</sub>, f<sub>1</sub>, f<sub>1</sub>‘), wobei eine unendliche Reihe von immer schwereren solcher Teilchen aufsummiert werden muss, um ein mathematisch konsistentes Modell zu erhalten. |
||
| + | </small> |
||
Im Jahr 2004 wiesen aber zwei russisch-stämmige Physiker aus den USA, Kirill Melnikov und Arkady Vainshtein, darauf hin, dass alle gängigen Modelle ein Problem mit dieser Extrapolation in einem gewissen Bereich bei hohen Energien und damit zusammenhängend bei kleinsten Abständen haben [1]. Die erwähnte Quantenanomalie ist nämlich in manchen dieser Bereiche exakt berechenbar, aber herkömmliche Modelle schafften es nicht, alle diese Bereiche gleichzeitig abzudecken. Melnikov und Vainshtein schlugen ihrerseits ein Modell vor, das dies korrigierte, und kamen zum Schluss, dass die hadronische Licht-an-Licht-Streuung viel größere Beiträge liefern könnte, als alle anderen Modelle vorhersagten. Das Melnikov-Vainshtein-Modell (MV) hatte aber eine andere Schwierigkeit – die universell gültige Impulserhaltung wurde dabei teilweise außer Kraft gesetzt, weshalb viele Physiker das MV-Modell nicht akzeptieren wollten, auch nicht für den Zweck, die theoretischen Unsicherheiten abzuschätzen. Dieser Konflikt bestand über all diese Jahre und wurde 2019 erneut thematisiert, als es darum ging, unter den Theoretikern einen weitgehenden Konsens über die finale theoretische Vorhersage herzustellen, die in einem sogenannten White Paper mit 132 Autoren [2] im Sommer 2020 publiziert wurde - vermeintlich kurz bevor das Fermilab-Experiment seine Ergebnisse enthüllen würde (was sich aber durch die Corona-Krise noch länger hinziehen sollte). |
Im Jahr 2004 wiesen aber zwei russisch-stämmige Physiker aus den USA, Kirill Melnikov und Arkady Vainshtein, darauf hin, dass alle gängigen Modelle ein Problem mit dieser Extrapolation in einem gewissen Bereich bei hohen Energien und damit zusammenhängend bei kleinsten Abständen haben [1]. Die erwähnte Quantenanomalie ist nämlich in manchen dieser Bereiche exakt berechenbar, aber herkömmliche Modelle schafften es nicht, alle diese Bereiche gleichzeitig abzudecken. Melnikov und Vainshtein schlugen ihrerseits ein Modell vor, das dies korrigierte, und kamen zum Schluss, dass die hadronische Licht-an-Licht-Streuung viel größere Beiträge liefern könnte, als alle anderen Modelle vorhersagten. Das Melnikov-Vainshtein-Modell (MV) hatte aber eine andere Schwierigkeit – die universell gültige Impulserhaltung wurde dabei teilweise außer Kraft gesetzt, weshalb viele Physiker das MV-Modell nicht akzeptieren wollten, auch nicht für den Zweck, die theoretischen Unsicherheiten abzuschätzen. Dieser Konflikt bestand über all diese Jahre und wurde 2019 erneut thematisiert, als es darum ging, unter den Theoretikern einen weitgehenden Konsens über die finale theoretische Vorhersage herzustellen, die in einem sogenannten White Paper mit 132 Autoren [2] im Sommer 2020 publiziert wurde - vermeintlich kurz bevor das Fermilab-Experiment seine Ergebnisse enthüllen würde (was sich aber durch die Corona-Krise noch länger hinziehen sollte). |
||
| Line 33: | Line 46: | ||
<h2>Wie unser Institut hier mitmischt</h2> |
<h2>Wie unser Institut hier mitmischt</h2> |
||
| − | An dieser Stelle kommt nun der Beitrag ins Spiel, der am Institut für Theoretische Physik der TU Wien von Prof. Anton Rebhan zusammen mit dem von ihm betreuten PhD-Studenten Josef Leutgeb geliefert wurde. Im Dezember 2019 wurde von ihnen ein Paper herausgebracht [3], in dem gezeigt wurde, dass Modelle, die auf Prinzipien der Stringtheorie beruhen, die Bedingungen von Melnikov und Vainshtein in natürlicher Weise erfüllen können. (Ein zuvor |
+ | An dieser Stelle kommt nun der Beitrag ins Spiel, der am Institut für Theoretische Physik der TU Wien von Prof. Anton Rebhan zusammen mit dem von ihm betreuten PhD-Studenten Josef Leutgeb geliefert wurde. Im Dezember 2019 wurde von ihnen ein Paper herausgebracht [3], in dem gezeigt wurde, dass Modelle, die auf Prinzipien der Stringtheorie beruhen, die Bedingungen von Melnikov und Vainshtein in natürlicher Weise erfüllen können. (Ein zuvor eigens dafür konstruiertes Modell einer Gruppe aus Bern [4] hatte dies zwar auch erreicht, konnte aber nicht den wichtigen theoretischen Grenzfall masseloser Quarks abdecken.) Leutgeb und Rebhan fanden, dass unendlich viele Teilchenanregungen aus der Klasse der sogenannten Axialvektormesonen aufsummiert werden müssen, was herkömmliche Modelle nicht leisten können. In den durch die Stringtheorie motivierten „holographischen“ Modellen wird ein höherdimensionaler gekrümmter Raum ins Spiel gebracht, in dem die notwendigen Symmetrien samt ihrer Quantenanomalien realisiert werden können und der in den gewöhnlichen vier Raumzeitdimensionen unendlich viele Quantenfelder zur Folge hat. Die Quantenanomalien werden dabei durch Pionen zusammen mit einem unendlichen Turm von Axialvektormesonen erzeugt. |
| + | Zur selben Erkenntnis gelangte unabhängig auch eine italienisch-deutsch-französische Gruppe von Theoretikern, die ihre Ergebnisse nur wenige Tage nach Leutgeb und Rebhan als Preprint herausbrachten [5]. Wie sich herausstellte, hatten sie schon viel länger als Leutgeb und Rebhan daran gearbeitet, waren aber – für sie unglücklicherweise – am Ende überholt worden. Auch ihre numerischen Ergebnisse stimmten mit denen von Leutgeb und Rebhan überein, die damit bestätigt wurden. Diese sind nun deutlich kleiner als die Werte, die das umstrittene MV-Modell lieferte, aber größer als alle Beiträge, die bislang den Axialvektormesonen zugetraut wurden. |
||
| + | |||
| + | Leutgeb und Rebhan konnten allerdings zeigen, dass die wenigen experimentellen Daten, die es zur Kopplung von Axialvektormesonen an Photonen gibt, von ihrem holographischen Modell in guter Näherung vorhergesagt werden, während die herkömmlichen Modelle, die es zu Axialvektormesonen gibt, diese Daten nur als Input verwenden und auf möglichst einfache Weise extrapolieren. Die viel kompliziertere Form der Wechselwirkungen, wie sie im holographischen Modell erscheint, wurde aber durch eine spätere amerikanisch-schweizerische Publikation [8] validiert. |
||
Für das erwähnte White Paper wurden die neuen Erkenntnisse von Leutgeb und Rebhan und ihrer italienisch-französischen Konkurrenz insofern verwendet, als sie halfen, das MV-Modell ad acta zu legen. Die erhaltenen Beiträge der Axialvektormesonen wurden aber nicht verwendet, nachdem sie einerseits mit den oberen Grenzen der gesamten Beiträge wie bislang abgeschätzt noch in Einklang zu bringen waren, andererseits wohl auch, weil man das in Arbeit befindliche Konsensresultat nicht nochmals aufschnüren wollte - einige frühere Ergebnisse zu Axialvektormesonen hätten dazu verworfen werden müssen. Mit den neuen Ergebnissen nähert sich die Standardmodell-Vorhersage für die Anomalie a<sub>µ</sub>=(g-2)/2 geringfügig dem Ergebnis des BNL-Experiments an, dafür reduziert sich der abgeschätzte Fehler, sodass die Diskrepanz in etwa gleich bleibt: |
Für das erwähnte White Paper wurden die neuen Erkenntnisse von Leutgeb und Rebhan und ihrer italienisch-französischen Konkurrenz insofern verwendet, als sie halfen, das MV-Modell ad acta zu legen. Die erhaltenen Beiträge der Axialvektormesonen wurden aber nicht verwendet, nachdem sie einerseits mit den oberen Grenzen der gesamten Beiträge wie bislang abgeschätzt noch in Einklang zu bringen waren, andererseits wohl auch, weil man das in Arbeit befindliche Konsensresultat nicht nochmals aufschnüren wollte - einige frühere Ergebnisse zu Axialvektormesonen hätten dazu verworfen werden müssen. Mit den neuen Ergebnissen nähert sich die Standardmodell-Vorhersage für die Anomalie a<sub>µ</sub>=(g-2)/2 geringfügig dem Ergebnis des BNL-Experiments an, dafür reduziert sich der abgeschätzte Fehler, sodass die Diskrepanz in etwa gleich bleibt: |
||
| Line 41: | Line 57: | ||
*BNL-Experiment (2001-2006) [7,2]: 116 592 089(63)×10<sup>-11</sup> |
*BNL-Experiment (2001-2006) [7,2]: 116 592 089(63)×10<sup>-11</sup> |
||
| − | Diese Diskrepanz von 3,7 Standardabweichungen (σ) bedeutet, dass mit 99,98% Wahrscheinlichkeit ausgeschlossen werden kann, dass statistische Fluktuationen in den experimentellen Daten dafür verantwortlich sein könnten. Für eine definitive Entdeckung wird in der Teilchenphysik üblicherweise eine Signifikanz von 5σ gefordert, wobei es wichtig ist, dass mehr als nur ein Experiment mit hinreichender Genauigkeit durchgeführt wurde. |
+ | Diese Diskrepanz von 3,7 Standardabweichungen (σ) bedeutet, dass mit 99,98% Wahrscheinlichkeit ausgeschlossen werden kann, dass statistische Fluktuationen in den experimentellen Daten dafür verantwortlich sein könnten. Für eine definitive Entdeckung wird in der Teilchenphysik üblicherweise eine Signifikanz von 5σ gefordert, wobei es wichtig ist, dass mehr als nur ein Experiment mit hinreichender Genauigkeit durchgeführt wurde. Neben statistischen Fluktuationen könnten nämlich auch unentdeckte systematische Fehler im Spiel sein. |
| + | [[image:Pdgmuong+.png|400px]]<br /> |
||
| ⚫ | Das neue Fermilab-Experiment zielt wie gesagt darauf ab, die experimentelle Unschärfe um bis zu einen Faktor 4 zu verkleinern. Es wird dafür in den kommenden Jahren stetig verbesserte Resultate liefern; ab 2024 soll auch ein Myon-(g-2)-Experiment in Japan (bei der J-PARC Muon Facility) hinzukommen, womit auch die theoretischen Modelle weiter getrieben werden müssen. |
||
| + | <small>Abweichung der Standardmodell-Vorhersagen vom BNL-Experiment (LR 2020: Korrektur des White-Paper-Theorieresultats [2] durch Leutgeb & Rebhan [3,6]) © [https://pdg.lbl.gov/2020/reviews/rpp2020-rev-g-2-muon-anom-mag-moment.pdf PDG], adaptiert von A. Rebhan</small> |
||
| ⚫ | Das neue Fermilab-Experiment zielt wie gesagt darauf ab, die experimentelle Unschärfe um bis zu einen Faktor 4 zu verkleinern. Es wird dafür in den kommenden Jahren stetig verbesserte Resultate liefern; ab 2024 soll auch ein Myon-(g-2)-Experiment in Japan (bei der [https://j-parc.jp/c/en/index.html J-PARC] Muon Facility) hinzukommen, womit auch die theoretischen Modelle weiter getrieben werden müssen. |
||
| ⚫ | Josef Leutgeb, der über ein vom FWF finanziertes Doktoratskolleg „Particles & Interactions“ an der TU Wien forschen kann, arbeitet jedenfalls weiter daran, die holographischen Vorhersagen zu verfeinern. Das nächste Ziel ist es, auch angeregte Pionen zu inkludieren; eine entsprechende Veröffentlichung ist in Vorbereitung. An der Universität Wien gibt es, geleitet von Massimiliano Procura, ebenfalls eine Arbeitsgruppe, die sich mit theoretischen Vorhersagen zum anomalen magnetischen Moment des |
||
| + | |||
| ⚫ | Josef Leutgeb, der über ein vom FWF finanziertes [http://www.dkpi.at/ Doktoratskolleg „Particles & Interactions“] an der TU Wien forschen kann, arbeitet jedenfalls weiter daran, die holographischen Vorhersagen zu verfeinern. Das nächste Ziel ist es, auch angeregte Pionen zu inkludieren; eine entsprechende Veröffentlichung ist in Vorbereitung. An der Universität Wien gibt es, geleitet von Massimiliano Procura, ebenfalls eine Arbeitsgruppe, die sich mit theoretischen Vorhersagen zum anomalen magnetischen Moment des Myons beschäftigt. Hier forscht Procuras Doktorand Jan Lüdtke (ebenfalls ein Mitglied des genannten Doktoratskollegs) an komplementären Fragestellungen [9]. (Die Forschungen zu den Axialvektormesonen an der TU Wien wurden in der Tat erst durch den wissenschaftlichen Austausch innerhalb dieses Doktoratskollegs angestoßen, das nun leider 2022 vorzeitig ausläuft, weil der Forschungsförderungsfond FWF im Jahr 2014 aus finanziellen Gründen beschloss, diese Förderschiene einzustellen.) |
||
<h2>Quo vadis?</h2> |
<h2>Quo vadis?</h2> |
||
| − | Momentan ist die spannendste Frage aber: Wird das Fermilab-Experiment die bestehende Diskrepanz von Theorie und Experiment bestätigen oder gar verschärfen und damit den stärksten Hinweis bisher auf „Neue Physik“ jenseits des Standardmodells der Teilchenphysik liefern? (Andere Hinweise, allerdings mit noch nicht so starken Abweichungen, haben sich erst kürzlich bei Experimenten mit den sogenannten B-Mesonen am CERN ergeben |
+ | Momentan ist die spannendste Frage aber: Wird das Fermilab-Experiment die bestehende Diskrepanz von Theorie und Experiment bestätigen oder gar verschärfen und damit den stärksten Hinweis bisher auf „Neue Physik“ jenseits des Standardmodells der Teilchenphysik liefern? ([https://home.cern/news/news/physics/intriguing-new-result-lhcb-experiment-cern Andere Hinweise], allerdings mit noch nicht so starken Abweichungen, haben sich erst kürzlich bei Experimenten mit den sogenannten B-Mesonen am CERN ergeben.) Oder wird diese Diskrepanz beim magnetischen Moment des Myons verschwinden und alles zu einem bittersüßen Triumph der Theoretiker machen, die damit weitere Mühen der Ebene vor sich haben werden, um hier die Grenzen des bestehenden Standardmodells aufzuspüren? |
| Line 66: | Line 85: | ||
[7] https://inspirehep.net/literature/552899, https://inspirehep.net/literature/710962 |
[7] https://inspirehep.net/literature/552899, https://inspirehep.net/literature/710962 |
||
| − | [8] https://inspirehep.net/literature/ |
+ | [8] https://inspirehep.net/literature/1791135 |
| + | |||
| + | [9] https://inspirehep.net/literature/1798637 |
||
| + | |||
| + | |||
| + | |||
| ⚫ | |||
| + | |||
| ⚫ | |||
| ⚫ | |||
| + | |||
| + | [[image:Fermilab-Screenshot.png|650px]] |
||
| + | |||
| + | Das neue Muon-g-2-Experiment am Fermilab hat also die Genauigkeit des alten BNL-Experiments erreicht und ein klein wenig übertroffen. Die Abweichung von der Standardmodell-Vorhersage ist zwar leicht reduziert, bleibt aber bestehen, bei nun 3,3 Standardabweichungen. Beide Experimente sind durch statistische Fehler dominiert. Kombiniert man die Datensätze, erhöht sich sogar die Signifikanz der Abweichung vom Standardmodell auf 4,2 Standardabweichungen. |
||
| + | |||
| + | Das Fermilab-Experiment hat allerdings bereits sehr viel mehr Daten genommen, als für dieses erste Ergebnis verwendet wurden. In 1½-2 Jahren soll das Ziel erreicht werden, die Genauigkeit um den angestrebten Faktor 4 zu erreichen. Bleiben Theorie und Experiment weiterhin innerhalb ihrer jeweiligen Fehlerbalken, sollte der kritische Pegel von 5 Standardabweichungen, der für eine definitive Entdeckung traditionell gefordert wird, dann erreicht sein. |
||
| + | |||
| + | * [https://www.youtube.com/watch?v=nrus0aIa94I Youtube video des Fermilab-Seminars] |
||
| + | ----- |
||
| − | [9] https://home.cern/news/news/physics/intriguing-new-result-lhcb-experiment-cern |
||
| + | '''PS: Zwei Theorie-Updates, auch am 7. April 2021 lanciert''' |
||
| + | Das Datum der Enthüllung der Fermilab-Ergebnisse haben auch zwei Gruppen von theoretischen Physikern genützt, um neue Resultate öffentlichkeitswirksam zu publizieren: |
||
| + | * Auf [https://www.nature.com/articles/s41586-021-03418-1 Nature] wurden die schon vor einem Jahr als Preprint erschienen Ergebnisse der sogenannten BMW-Kollaboration (Budapest-Marseille-Wuppertal) publiziert, die in numerischen Simulationen einen vom Theorie-Konsens abweichenden höheren Beitrag der oben kurz erwähnten hadronischen Vakuumpolarisation erhielten. Dieser würde die Diskrepanz zwischen Standardmodell und den g-2-Experimenten fast komplett eliminieren. |
||
| ⚫ | |||
| + | : Allerdings wurde bereits letztes Jahr in [https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.125.091801 dieser Publikation] (und auch [https://journals.aps.org/prd/abstract/10.1103/PhysRevD.102.033002 hier]) darauf hingewiesen, dass es damit an einer anderen Stelle zu Diskrepanzen zwischen Theorie und Experiment kommen würde, nämlich bei den Präzisionsexperimenten zur elektroschwachen Wechselwirkung. |
||
| ⚫ | |||
| + | : Es bleibt abzuwarten, ob andere Gruppen die Ergebnisse der BMW-Gruppe mit der von letzterer behaupteten Genauigkeit reproduzieren können, wie auch die [https://www.nature.com/articles/d41586-021-00898-z Nature News Meldung] dazu hervorhebt und stattdessen die Hinweise auf Neue Physik betont. |
||
| ⚫ | |||
| + | * Zur oben hauptsächlich besprochenen hadronischen Licht-an-Lichtstreuung und ihrem Beitrag zum Myon-Magnetismus erschienen ebenfalls neue Resultate von numerischen Simulationen als [https://arxiv.org/abs/2104.02632 Preprint]. Diese bestätigen aber die bisherigen theoretischen Ergebnisse innerhalb der abgeschätzten Fehler. Numerisch sind die neuen Ergebnisse allerdings etwas größer und passen damit perfekt zu den Ergebnissen von Leutgeb und Rebhan, denen zufolge der Beitrag von Axialvektormesonen zuvor unterschätzt wurde. |
||
| − | und dann an dieser Stelle weitergegeben. |
||
Latest revision as of 19:26, 8 April 2021
Eine etwas längliche Geschichte über einen kleinen Teil eines winzigen Effektes, der Teilchenphysiker in aufgeregter Spannung hält, und zu dem es nach fast 20-jährigem Warten am 7. April 2021 neue Resultate von einem Experiment am Fermilab bei Chicago gibt:
Das anomale magnetische Moment von Myonen und anomale Licht-an-Licht-Streuung: Hinweise auf „Neue Physik“?
Vom Elektron zum Myon
Um diese Geschichte einordnen zu können, muss zuerst die Erfolgsgeschichte der Quantenelektrodynamik rekapituliert werden, die um das anomale magnetische Moment von Elektronen geschrieben wurde: 1928 fand Paul Dirac die fundamentale Gleichung, mit der die spezielle Relativitätstheorie mit den Wellengleichungen, wie sie Schrödinger zuvor gefunden hatte, in Einklang gebracht werden kann, um Elementarteilchen mit elektrischer Ladung und Spin konsistent zu beschreiben. Die Dirac-Gleichung impliziert, dass Elektronen ein magnetisches Dipolmoment haben, das zum Spin proportional ist, allerdings mit einem zusätzlichen Erhöhungsfaktor g=2 im Vergleich zum Zusammenhang von Bahndrehimpuls und magnetischem Dipolmoment – ein Umstand, der schon zuvor bekannt, aber unverstanden geblieben war. Diese Verdoppelung stellte sich somit als direkte Konsequenz der speziellen Relativitätstheorie heraus, die unabhängig davon ist, ob sich Elektronen schnell oder langsam bewegen.
In den folgenden Jahren wurde die von Dirac begründete relativistische Quantenmechanik zur Quantenfeldtheorie weiterentwickelt, in der es keine feste Anzahl von Teilchen mehr gibt, sondern Quantenfluktuationen kurzfristig “virtuelle” Teilchen-Antiteilchen-Paare und Photonen ins Spiel bringen. Diese führen dazu, dass das vermeintlich exakte Resultat g=2 geringfügig abgeändert wird, und zwar um 0.116% erhöht, wie der Nobelpreisträger Julian Schwinger 1948 als erster berechnet hatte. Schwingers elegantes Resultat für diese sogenannte Anomalie des magnetischen Moments des Elektrons, das auch seinen Grabstein ziert (α/2π = 0.00116…), ist allerdings nur eine erste, wenn auch sehr präzise Näherung.
Mittlerweile konnte das magnetische Moment des Elektrons (genauer, der g-Faktor) mit einer Genauigkeit von besser als 1:1012 vermessen werden und parallel dazu die Genauigkeit der theoretischen Vorhersage ebenso auf 12 Stellen nach dem Komma gesteigert werden. Die Übereinstimmung von Theorie und Experiment stellt einen der größten Triumphe der modernen Physik dar.
In den enorm aufwändigen Rechnungen dazu, die Jahrzehnte in Anspruch genommen haben, müssen unter anderem Prozesse berücksichtigt werden, bei denen virtuelle Photonen an anderen virtuellen Photonen gestreut werden. Eine solche Streuung von Licht an Licht ist ein rein quantenfeldtheoretischer Effekt, der weder in der klassischen Elektrodynamik noch in “gewöhnlicher” Quantenmechanik möglich ist. Direkt konnte die Licht-an-Licht-Streuung erst vor ein paar Jahren im Zusammenhang mit Schwerionenkollisionen am CERN beobachtet werden, aber indirekt war sie schon längst durch die Übereinstimmung von Theorie und Experiment beim anomalen magnetischen Moment des Elektrons nachgewiesen worden – als ein quantenfeldtheoretischer Effekt unter vielen. Diese virtuellen Prozesse involvieren nicht nur Photonen, Elektronen und Positronen, sondern im Prinzip alle Elementarteilchen, die es überhaupt gibt - allerdings mit umso kleineren Effekten, je schwerer sie sind, denn umso kurzlebiger sind sie als virtuelle Teilchen.
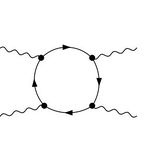
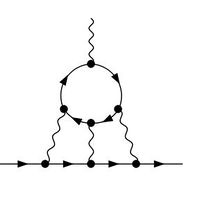
Links: Licht-an-Licht-Streuung von reellen Photonen (Wellenlinien) durch eine Schleife in der Raumzeit, die von virtuellen Elektronen (Linien mit Pfeil) gebildet wird.
Rechts: Licht-an-Licht-Streuung in der Wechselwirkung eines reellen Photons mit einem reellen geladenen Teilchen (unterste Linie) modifiziert dessen magnetisches Moment
Beim Elektron kommt man allerdings erst nach der 12. Stelle hinter dem Komma in den Bereich, wo eventuelle Physik jenseits des gegenwärtigen Standardmodells eine Rolle spielen könnte, und bislang gibt es eine nahezu perfekte Übereinstimmung von herkömmlicher Theorie und Experiment (mit einer leichten interessanten Diskrepanz, die das Ziel weiterer verfeinerter Experimente ist).
Ein anderes Elementarteilchen, dessen magnetisches Moment mit ähnlichem Aufwand studiert wurde, ist das Myon. Myonen sind Elementarteilchen, die Elektronen in jeder Hinsicht ähneln, aber etwa 200mal schwerer sind. Ihr anomales magnetisches Moment ist dadurch um einiges sensitiver auf Prozesse mit schweren virtuellen Teilchen. Allerdings ist ihr magnetisches Moment weit schwieriger zu messen, weil Myonen nur einige Mikrosekunden Lebensdauer haben und in Elektronen und Neutrinos zerfallen. Das beste experimentelle Resultat bislang wurde Anfang der 2000er-Jahre in einem Speicherring für Myonen am Brookhaven National Lab (BNL) erzielt, mit dem aufsehenerregenden Ergebnis, dass Theorie und Experiment “schon” in der 9. Stelle nach dem Komma abweichen, mit einer Diskrepanz, die 3.7 Standardabweichungen entspricht.

BNL-Experiment mit supraleitendem Ringmagnet (blau) © BNL, https://www.g-2.bnl.gov/pictures/index.html
Das neue Experiment am FERMILAB und neuere theoretische Entwicklungen
Am Fermilab bei Chicago wurde seit 2013 das 700 Tonnen schwere BNL-Experiment neu aufgebaut, siehe https://muon-g-2.fnal.gov/. Dazu wurde der am BNL geschaffene supraleitende Magnet mit einem Durchmesser von 15 Metern von Long Island im Bundesstaat New York über den Golf von Mexiko und den Mississippi hinauf und weiter auf dem Landweg nach Batavia, Illinois, transportiert. Dieser Magnet ist dafür ausgelegt, ein möglichst starkes und möglichst homogenes Magnetfeld zu liefern, in dem sich die am Fermilab-Beschleuniger produzierten instabilen Myonen auf einer Kreisbahn bewegen. Dabei kommt es zu einer Präzession (d.h. ein Kreiseln) ihres Spins, die mit hoher Genauigkeit (Präzision) gemessen wird. 2018 war der Wiederaufbau eines verbesserten Experiments abgeschlossen und es konnte mit diesen Messungen begonnen werden. Diese sind für mehrere Jahre ausgelegt, mit dem Ziel, die Genauigkeit bis zu einem Faktor 4 gegenüber dem BNL-Experiment zu steigern.
Am 7. April 2021 werden die ersten Ergebnisse dazu der Öffentlichkeit präsentiert. Falls schon in etwa die Genauigkeit des BNL-Resultats erreicht oder sogar übertroffen wurde, lässt sich endlich mehr dazu sagen, ob das anomale magnetische Moment des Myons Beiträge von „Neuer Physik“, jenseits des Standardmodells aufweist. Dazu muss natürlich auch die theoretische Vorhersage des Standardmodells eine mindestens so hohe Präzision garantieren können.
In den letzten zwei Jahrzehnten haben mehr als hundert theoretische Physiker daran gearbeitet, die theoretischen Ergebnisse zu verbessern. Zwei physikalische Phänomene, die es zu berücksichtigen gab, bildeten dabei die hauptsächliche Schwierigkeit, deren Präzision zu verbessern. Bei beiden geht es um die Wechselwirkung von virtuellen Photonen mit stark selbst-wechselwirkenden Elementarteilchen, den sogenannten Hadronen, die als Quantenfluktuationen im Vakuum präsent sind. Myonen spüren wegen ihrer größeren Masse deren Effekte viel stärker als die leichten Elektronen.
Der größere der beiden Effekte ist die hadronische Vakuumpolarisation, die über Beschleunigerexperimente indirekt vermessen werden kann und deren Präzision über die Jahre beständig gesteigert wurde.
Ein weit kleinerer, aber mit größeren Unsicherheiten behafteter Effekt ist die hadronische Licht-an-Licht-Streuung, bei der vier virtuelle Photonen zusammenkommen. Der Hauptbeitrag dazu ist ein Prozess, der selbst eine Anomalie darstellt: der Zerfall eines neutralen Pions (π0) in zwei Photonen bzw. die Produktion eines Pions über zwei Photonen. Diesen Prozess dürfte es in der beobachteten Stärke aus Symmetriegründen eigentlich nicht geben. Quantenfluktuationen können aber Symmetrien aufbrechen, in diesem Fall die sogenannte chirale Symmetrie, die rechts- und linkshändige Quarks gegengleich „rotiert“. Für die Wechselwirkung dieser Pionen mit virtuellen Photonen gibt es zumindest teilweise experimentelle Daten, die für die notwendigen Rechnungen aber extrapoliert werden müssen, und dafür wurden immer stärker verfeinerte Modelle entwickelt.

Licht-an-Licht-Streuung an Quantenfluktuationen mit stark wechselwirkenden Quarks und Gluonen und von ihnen gebildeten Elementarteilchen.
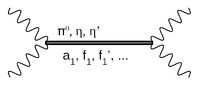
Hauptbeitrag dabei ist die Erzeugung und der Zerfall eines virtuellen Pions (π0) und ähnlicher (sog. pseudoskalarer) Teilchen (η, η'), die durch die chirale Quantenanomalie bestimmt werden. Letztere führt aber auch zu einem verstärkten Beitrag von sogenannten Axialvektorrmesonen (a1, f1, f1‘), wobei eine unendliche Reihe von immer schwereren solcher Teilchen aufsummiert werden muss, um ein mathematisch konsistentes Modell zu erhalten.
Im Jahr 2004 wiesen aber zwei russisch-stämmige Physiker aus den USA, Kirill Melnikov und Arkady Vainshtein, darauf hin, dass alle gängigen Modelle ein Problem mit dieser Extrapolation in einem gewissen Bereich bei hohen Energien und damit zusammenhängend bei kleinsten Abständen haben [1]. Die erwähnte Quantenanomalie ist nämlich in manchen dieser Bereiche exakt berechenbar, aber herkömmliche Modelle schafften es nicht, alle diese Bereiche gleichzeitig abzudecken. Melnikov und Vainshtein schlugen ihrerseits ein Modell vor, das dies korrigierte, und kamen zum Schluss, dass die hadronische Licht-an-Licht-Streuung viel größere Beiträge liefern könnte, als alle anderen Modelle vorhersagten. Das Melnikov-Vainshtein-Modell (MV) hatte aber eine andere Schwierigkeit – die universell gültige Impulserhaltung wurde dabei teilweise außer Kraft gesetzt, weshalb viele Physiker das MV-Modell nicht akzeptieren wollten, auch nicht für den Zweck, die theoretischen Unsicherheiten abzuschätzen. Dieser Konflikt bestand über all diese Jahre und wurde 2019 erneut thematisiert, als es darum ging, unter den Theoretikern einen weitgehenden Konsens über die finale theoretische Vorhersage herzustellen, die in einem sogenannten White Paper mit 132 Autoren [2] im Sommer 2020 publiziert wurde - vermeintlich kurz bevor das Fermilab-Experiment seine Ergebnisse enthüllen würde (was sich aber durch die Corona-Krise noch länger hinziehen sollte).
Wie unser Institut hier mitmischt
An dieser Stelle kommt nun der Beitrag ins Spiel, der am Institut für Theoretische Physik der TU Wien von Prof. Anton Rebhan zusammen mit dem von ihm betreuten PhD-Studenten Josef Leutgeb geliefert wurde. Im Dezember 2019 wurde von ihnen ein Paper herausgebracht [3], in dem gezeigt wurde, dass Modelle, die auf Prinzipien der Stringtheorie beruhen, die Bedingungen von Melnikov und Vainshtein in natürlicher Weise erfüllen können. (Ein zuvor eigens dafür konstruiertes Modell einer Gruppe aus Bern [4] hatte dies zwar auch erreicht, konnte aber nicht den wichtigen theoretischen Grenzfall masseloser Quarks abdecken.) Leutgeb und Rebhan fanden, dass unendlich viele Teilchenanregungen aus der Klasse der sogenannten Axialvektormesonen aufsummiert werden müssen, was herkömmliche Modelle nicht leisten können. In den durch die Stringtheorie motivierten „holographischen“ Modellen wird ein höherdimensionaler gekrümmter Raum ins Spiel gebracht, in dem die notwendigen Symmetrien samt ihrer Quantenanomalien realisiert werden können und der in den gewöhnlichen vier Raumzeitdimensionen unendlich viele Quantenfelder zur Folge hat. Die Quantenanomalien werden dabei durch Pionen zusammen mit einem unendlichen Turm von Axialvektormesonen erzeugt. Zur selben Erkenntnis gelangte unabhängig auch eine italienisch-deutsch-französische Gruppe von Theoretikern, die ihre Ergebnisse nur wenige Tage nach Leutgeb und Rebhan als Preprint herausbrachten [5]. Wie sich herausstellte, hatten sie schon viel länger als Leutgeb und Rebhan daran gearbeitet, waren aber – für sie unglücklicherweise – am Ende überholt worden. Auch ihre numerischen Ergebnisse stimmten mit denen von Leutgeb und Rebhan überein, die damit bestätigt wurden. Diese sind nun deutlich kleiner als die Werte, die das umstrittene MV-Modell lieferte, aber größer als alle Beiträge, die bislang den Axialvektormesonen zugetraut wurden.
Leutgeb und Rebhan konnten allerdings zeigen, dass die wenigen experimentellen Daten, die es zur Kopplung von Axialvektormesonen an Photonen gibt, von ihrem holographischen Modell in guter Näherung vorhergesagt werden, während die herkömmlichen Modelle, die es zu Axialvektormesonen gibt, diese Daten nur als Input verwenden und auf möglichst einfache Weise extrapolieren. Die viel kompliziertere Form der Wechselwirkungen, wie sie im holographischen Modell erscheint, wurde aber durch eine spätere amerikanisch-schweizerische Publikation [8] validiert.
Für das erwähnte White Paper wurden die neuen Erkenntnisse von Leutgeb und Rebhan und ihrer italienisch-französischen Konkurrenz insofern verwendet, als sie halfen, das MV-Modell ad acta zu legen. Die erhaltenen Beiträge der Axialvektormesonen wurden aber nicht verwendet, nachdem sie einerseits mit den oberen Grenzen der gesamten Beiträge wie bislang abgeschätzt noch in Einklang zu bringen waren, andererseits wohl auch, weil man das in Arbeit befindliche Konsensresultat nicht nochmals aufschnüren wollte - einige frühere Ergebnisse zu Axialvektormesonen hätten dazu verworfen werden müssen. Mit den neuen Ergebnissen nähert sich die Standardmodell-Vorhersage für die Anomalie aµ=(g-2)/2 geringfügig dem Ergebnis des BNL-Experiments an, dafür reduziert sich der abgeschätzte Fehler, sodass die Diskrepanz in etwa gleich bleibt:
- White Paper Standardmodell-Vorhersage für die Anomalie aµ [2]: 116 591 810(43)×10-11
- Selbiges mit Axialvektorresultaten von Leutgeb und Rebhan [3,6]: 116 591 824(33)×10-11
- BNL-Experiment (2001-2006) [7,2]: 116 592 089(63)×10-11
Diese Diskrepanz von 3,7 Standardabweichungen (σ) bedeutet, dass mit 99,98% Wahrscheinlichkeit ausgeschlossen werden kann, dass statistische Fluktuationen in den experimentellen Daten dafür verantwortlich sein könnten. Für eine definitive Entdeckung wird in der Teilchenphysik üblicherweise eine Signifikanz von 5σ gefordert, wobei es wichtig ist, dass mehr als nur ein Experiment mit hinreichender Genauigkeit durchgeführt wurde. Neben statistischen Fluktuationen könnten nämlich auch unentdeckte systematische Fehler im Spiel sein.
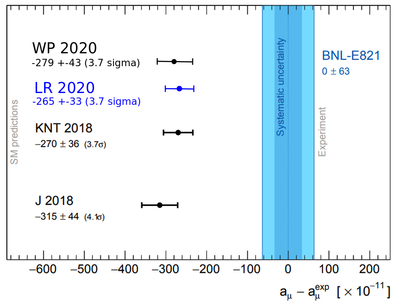
Abweichung der Standardmodell-Vorhersagen vom BNL-Experiment (LR 2020: Korrektur des White-Paper-Theorieresultats [2] durch Leutgeb & Rebhan [3,6]) © PDG, adaptiert von A. Rebhan
Das neue Fermilab-Experiment zielt wie gesagt darauf ab, die experimentelle Unschärfe um bis zu einen Faktor 4 zu verkleinern. Es wird dafür in den kommenden Jahren stetig verbesserte Resultate liefern; ab 2024 soll auch ein Myon-(g-2)-Experiment in Japan (bei der J-PARC Muon Facility) hinzukommen, womit auch die theoretischen Modelle weiter getrieben werden müssen.
Josef Leutgeb, der über ein vom FWF finanziertes Doktoratskolleg „Particles & Interactions“ an der TU Wien forschen kann, arbeitet jedenfalls weiter daran, die holographischen Vorhersagen zu verfeinern. Das nächste Ziel ist es, auch angeregte Pionen zu inkludieren; eine entsprechende Veröffentlichung ist in Vorbereitung. An der Universität Wien gibt es, geleitet von Massimiliano Procura, ebenfalls eine Arbeitsgruppe, die sich mit theoretischen Vorhersagen zum anomalen magnetischen Moment des Myons beschäftigt. Hier forscht Procuras Doktorand Jan Lüdtke (ebenfalls ein Mitglied des genannten Doktoratskollegs) an komplementären Fragestellungen [9]. (Die Forschungen zu den Axialvektormesonen an der TU Wien wurden in der Tat erst durch den wissenschaftlichen Austausch innerhalb dieses Doktoratskollegs angestoßen, das nun leider 2022 vorzeitig ausläuft, weil der Forschungsförderungsfond FWF im Jahr 2014 aus finanziellen Gründen beschloss, diese Förderschiene einzustellen.)
Quo vadis?
Momentan ist die spannendste Frage aber: Wird das Fermilab-Experiment die bestehende Diskrepanz von Theorie und Experiment bestätigen oder gar verschärfen und damit den stärksten Hinweis bisher auf „Neue Physik“ jenseits des Standardmodells der Teilchenphysik liefern? (Andere Hinweise, allerdings mit noch nicht so starken Abweichungen, haben sich erst kürzlich bei Experimenten mit den sogenannten B-Mesonen am CERN ergeben.) Oder wird diese Diskrepanz beim magnetischen Moment des Myons verschwinden und alles zu einem bittersüßen Triumph der Theoretiker machen, die damit weitere Mühen der Ebene vor sich haben werden, um hier die Grenzen des bestehenden Standardmodells aufzuspüren?
[1] https://inspirehep.net/literature/635797
[2] https://inspirehep.net/literature/1800513
[3] https://inspirehep.net/literature/1768266
[4] https://inspirehep.net/literature/1761991
[5] https://inspirehep.net/literature/1768687
[6] https://inspirehep.net/literature/1836285
[7] https://inspirehep.net/literature/552899, https://inspirehep.net/literature/710962
[8] https://inspirehep.net/literature/1791135
[9] https://inspirehep.net/literature/1798637
UPDATE (vom 7. April 2021)
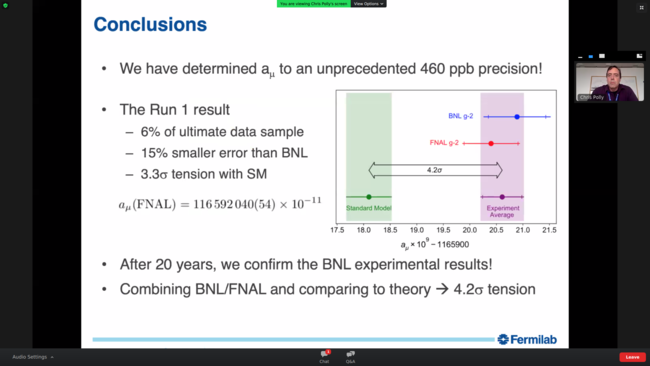
Am 7. April 2021, 10 Uhr Chicago-Zeit, 17 Uhr MEST, wurden bei einem speziellen Seminar am Fermilab die ersten Resultate des neuen Muon g-2 Experiment enthüllt:
Das neue Muon-g-2-Experiment am Fermilab hat also die Genauigkeit des alten BNL-Experiments erreicht und ein klein wenig übertroffen. Die Abweichung von der Standardmodell-Vorhersage ist zwar leicht reduziert, bleibt aber bestehen, bei nun 3,3 Standardabweichungen. Beide Experimente sind durch statistische Fehler dominiert. Kombiniert man die Datensätze, erhöht sich sogar die Signifikanz der Abweichung vom Standardmodell auf 4,2 Standardabweichungen.
Das Fermilab-Experiment hat allerdings bereits sehr viel mehr Daten genommen, als für dieses erste Ergebnis verwendet wurden. In 1½-2 Jahren soll das Ziel erreicht werden, die Genauigkeit um den angestrebten Faktor 4 zu erreichen. Bleiben Theorie und Experiment weiterhin innerhalb ihrer jeweiligen Fehlerbalken, sollte der kritische Pegel von 5 Standardabweichungen, der für eine definitive Entdeckung traditionell gefordert wird, dann erreicht sein.
PS: Zwei Theorie-Updates, auch am 7. April 2021 lanciert
Das Datum der Enthüllung der Fermilab-Ergebnisse haben auch zwei Gruppen von theoretischen Physikern genützt, um neue Resultate öffentlichkeitswirksam zu publizieren:
- Auf Nature wurden die schon vor einem Jahr als Preprint erschienen Ergebnisse der sogenannten BMW-Kollaboration (Budapest-Marseille-Wuppertal) publiziert, die in numerischen Simulationen einen vom Theorie-Konsens abweichenden höheren Beitrag der oben kurz erwähnten hadronischen Vakuumpolarisation erhielten. Dieser würde die Diskrepanz zwischen Standardmodell und den g-2-Experimenten fast komplett eliminieren.
- Allerdings wurde bereits letztes Jahr in dieser Publikation (und auch hier) darauf hingewiesen, dass es damit an einer anderen Stelle zu Diskrepanzen zwischen Theorie und Experiment kommen würde, nämlich bei den Präzisionsexperimenten zur elektroschwachen Wechselwirkung.
- Es bleibt abzuwarten, ob andere Gruppen die Ergebnisse der BMW-Gruppe mit der von letzterer behaupteten Genauigkeit reproduzieren können, wie auch die Nature News Meldung dazu hervorhebt und stattdessen die Hinweise auf Neue Physik betont.
- Zur oben hauptsächlich besprochenen hadronischen Licht-an-Lichtstreuung und ihrem Beitrag zum Myon-Magnetismus erschienen ebenfalls neue Resultate von numerischen Simulationen als Preprint. Diese bestätigen aber die bisherigen theoretischen Ergebnisse innerhalb der abgeschätzten Fehler. Numerisch sind die neuen Ergebnisse allerdings etwas größer und passen damit perfekt zu den Ergebnissen von Leutgeb und Rebhan, denen zufolge der Beitrag von Axialvektormesonen zuvor unterschätzt wurde.