
Fundamental Interactions
According to our present knowledge there are four fundamental interactions in nature: gravity, electromagnetism, weak and strong interaction with electromagnetism and weak interaction unified in the electroweak theory. Gravity as well as electromagnetism are macroscopic phenomena, immediately present in our everyday life, like falling objects and static electricity. Weak and strong nuclear interactions, on the other hand, become only important on the microscopic, atomic and subatomic level.
The most important aspect of the strong interaction is that it provides stability to the nucleus overcoming electric repulsion, whereas the transmutation of neutrons into protons is the most well-known weak phenomenon. The aim of fundamental physics may be described as obtaining a deeper understanding of these interactions, and penultimately finding a unified framework, which understands the different interactions as different aspects of a single truly fundamental interaction.
Research topics
Quantum field theory and non-commutative geometry
Describing the interactions on a more fundamental level the concepts of relativistic quantum field theories are employed. With the advent of quantum mechanics in the first decades of the 20th century it was realized that the electromagnetic field, including light, is quantized and can be seen as a stream of particles, the photons. This implies that the interaction between matter is mediated by the exchange of photons. The concept of relativistic quantum field theory is very simple, unifying a classical field theory with the concepts of quantum theory and special relativity.
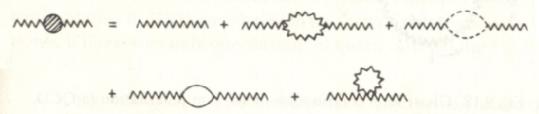
Fig.: Full propagator in terms of free propagation and self-energy corrections.
The construction of the perturbative NCQFT leads to new types of infrared (IR) singularities which represent a severe obstacle for the renormalization program at higher order and therefore lead to inconsistencies. The IR singularities are produced by the so-called UV finite nonplanar one-loop graphs (which are expected to be UV divergent by naive power counting) in U(N) gauge models and also in scalar field theories. The interplay between expected UV divergencies and the existence of the IR singularities is the so-called UV/IR mixing problem of NCQFT. One also has to stress that the usual UV divergences may be removed by the standard renormalization procedure.
The present research activities are devoted to find solutions for the UV/IR mixing problem of noncommutative gauge field models. In order to respect the effects of noncommutativity implied by the non-abelian structure a consistent treatment requires the use of the BRS quantization procedure even for a U(1) deformed Maxwell theory.
Gravitation
Since the groundbreaking work of Einstein, gravitation is conceived as defining the geometry of spacetime - even defining the very concepts of time and space itself. Planetary motion as well as the motion of massless particles, that is to say light, become the straightest possible paths in a non-Euclidean geometry.
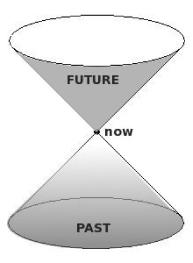
Fig.: Light-cone of an event representing its causal past and future.
General relativity is a very successful theory. Its predictions range from the deflection of light by massive bodies which distort spacetime (Einstein-lensing) to that of gravitational radiation carrying away energy in the form of "ripples" in spacetime (Hulse-Taylor binary pulsar), as well as to the expansion of the universe (microwave background radiation). One of the most spectacular predictions of general relativity is the existence of black holes, which by now has been confirmed indirectly by numerous astrophysical observations.
Despite of these successes there are several unresolved problems in the physics of gravitation, some of which are considered as the biggest problems in contemporary theoretical physics:
- The cosmological constant problem entails a gigantic discrepancy (123 orders of magnitude) between observation and naive theoretical expectation, and so far no satisfying explanation exists that resolves this discrepancy.
- Numerous astrophysical and cosmological observations reveal discrepancies with the theory of general relativity, unless we postulate the existence of dark matter, which so far has not been detected in particle physics experiments.
- The elusive theory of quantum gravity still is very much a theory under construction, with several conceptual and technical issues seeking for solutions.
- General relativity predicts its own failure as a consequence of the famous singularity theorems. Physically this means that spacetime contains regions where the curvature grows without a bound. The most prominent examples are the singularities within black holes as well as the Big Bang singularity.
Deeper insights into the structure of physical systems have often been achieved by the imposition of symmetries. This usually breaks the problem down into simpler building blocks which ideally allow a complete solution. Gravity is no exception to this rule since the prototypic black-hole solution, the Schwarzschild geometry (actually the first exact non-trivial solution of the Einstein-equations), has been found precisely along theses lines, i.e. upon imposing spherical symmetry. It is therefore natural to pursue a similar plan of attack for the quantization of gravity. The corresponding models become gravitational theories in a 1+1 dimensional spacetime coupled to the area of the two-sphere which becomes a dynamical variable in the reduced theory. There are several other ways how lowerdimensional (1+1 and 2+1) models arise from higherdimensional configurations in string theory or general relativity, and the description of gravity in lower dimensions is one of the key research fields of our group.
Quark-Gluon plasma
Quantum chromodynamics (QCD) is the accepted theory of the strong interactions responsible for the binding of quarks into hadrons such as protons and neutrons, and the binding of protons and neutrons into atomic nuclei. The fundamental particles of QCD, the quarks and gluons, carry a new form of charge, which is called color because of its triplet nature in the case of the quarks (e.g. red, green, blue); gluons come in eight different colors which are composites of color and anticolor charges. However, quarks and gluons have never been observed as free particles. Nevertheless, because quarks have also electrical charge, they can literally be seen as constituents of hadrons by deep inelastic scattering using virtual photons. The higher the energy of the probing photon, the more do the quarks appear as particles propagating freely within a hadron. This feature is called "asymptotic freedom". It arises from so-called nonabelian gauge field dynamics, with gluons being the excitations of the nonabelian gauge fields similarly to photons being the excitations of the electromagnetic fields, except that gluons also carry color charges. Asymptotic freedom is well understood, and the Nobel prize was awarded to its main discoverers Gross, Politzer, and Wilczek in 2004.
Much less understood is the phenomenon of "confinement", which means that only color-neutral bound states of quarks and gluons exist. This confinement can in fact be broken in a medium if the density exceeds significantly that of nuclear matter. When hadrons overlap so strongly that they loose their individuality, quarks and gluons come into their own as the elementary degrees of freedom. It is conceivable that such conditions are realized in the cores of certain neutron stars.
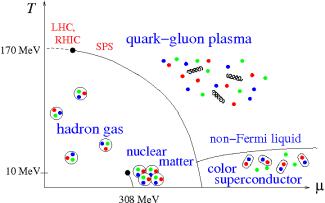
Fig.: Qualitative sketch of the phase diagram of quark-gluon matter as a function of temperature T and quark chemical potential µ. Solid lines denote rst-order phase transitions, the dashed line a rapid crossover.
At comparatively low temperatures, quark matter is known to form Cooper pairs and turns into a color superconductor. Also at temperatures just above the superconductivity phase new phenomena appear, which reflect that quark matter has strong deviations from an ideal Fermi liquid. In particular, there is anomalous behaviour in the low-temperature specific heat, which has been calculated for the first time systematically by our group. This has already found application in revised calculations of the cooling behavior of young neutron stars.
String theory
The names of the fundamental forces are related to their strength. The strong force is much stronger than electromagnetism and is thus able to overcome the repulsive force between objects with the same electrical charge (protons or quarks). The weak force is weaker than electromagnetism but still much stronger than gravity. The reason that we almost only recognize gravity in everyday life is that the macroscopic objects are neutral. They don't carry an effective color charge and they carry - if at all - only very small electric charges. For gravity there is no negative charge (negative mass), so that all the small gravitational effects add up to something which is strong enough to move galaxies and build black holes. The seperate description of the forces is quite accurate by now. This is summarized in the standard model of particle physics.
There is only one particle (the Higgs boson), which is predicted by the standard model and has not yet been found. A measure for the strength of a force are the coupling constants of the corresponding theory. They are, however, not constant, but depend on the energy level one is dealing with. If one extrapolates their values to high energies, one discovers that the couplings of electromagnetism, strong and weak force meet at a certain energy level almost in one single point (see Figure 1). This supports the idea that those three forces could be just different aspects of one and the same universal force. There are several theories which try to describe this unification. They are called GUTs, 'grand unified theories'. However, to be really 'grand', such a unification should also include gravity, whose coupling constant is far weaker still at this high energies. The theory, which will manage to unify all forces, including gravity, is sometimes called TOE, "theory of everything". String theory is one candidate, and at present actually the only one for this TOE.
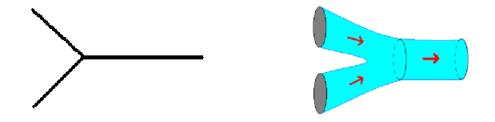
Fig.: Left: Point particle interaction, Right: Closed string interaction, note the smooth interaction surface.
'SUSY' stands for supersymmetry and means that there is an exchange symmetry between fermionic particles (like quarks and electrons) and bosonic ones (like photons and even gravitons, if one includes gravity into the considerations). It does, however, not relate the already known particles, but it predicts new supersymmetric partners to the known particles (called e.g. squarks, selectrons, photinos and gravitinos). So far none of those superparticles has been discovered, but there are a lot of theoretical reasons for believing in supersymmetry. Supersymmetry is an integral part of string theory, or more precisely 'superstring theory'. Within one year now, the new accelerator LHC (large hadron collider) at CERN will start and try to produce the Higgs boson and the superparticles mentioned above and will therefore also be a first test for string theory.
For further information and news on fundamental physics visit:
This contains the public outreach web pages of the Fachausschuss für Kern- und Teilchenphysik (FAKT) of the ÖPG (Austrian Physical Society), which our institute are hosting.
Preprints
Preprints of the group Fundamental Interactions:
Current year
- TUW-10-01 D.N. Blaschke, E. Kronberger, R.I.P. Sedmik and M. Wohlgenannt, Gauge Theories on Deformed Spaces hep-th/1004.2127
- TUW-10-02 V.G. Filev and R.C. Rashkov, Magnetic Catalysis of Chiral Symmetry Breaking. A Holographic Prospective. hep-th/100x.xxxx
- TUW-10-03 S. Ertl, D. Grumiller and N. Johansson, TBA hep-th/1005.xxxx
- TUW-10-04 A. Gynther, K. Landsteiner, F. Pena-Benitez and A. Rebhan, Holographic Anomalous Conductivities and the Chiral Magnetic Effect hep-th/1005.2587
- TUW-10-05 C. P. Herzog, S. A. Stricker and A. Vuorinen, Hyperfine splitting and the Zeeman effect in holographic heavy-light mesons hep-th/1005.3285
- TUW-10-06 C.-M. Chen and Y.-C. Chung, Flipped SU(5) GUTs from E8 singularity in F-theory hep-th/1005.5728
- TUW-10-07 C.-M. Chen , J. Knapp , M. Kreuzer and C. Mayrhofer, Global SO(10) F-theory GUTs hep-th/1005.5735
- TUW-10-08 M. Schweda and M. Wohlgenannt, On NCQFT and dimensionless insertions hep-th/1005.5107
- TUW-10-09 D. Arnaudov, H. Dimov and R.C. Rashkov, On the pulsating strings in $AdS_5\times T^{1,1}$ hep-th/1005.5334
- TUW-10-10 Jean-Paul Blaizot, Andreas Ipp, Nicolás Wschebor, Calculation of the pressure of a hot scalar theory within the Non-Perturbative Renormalization Group hep-th/1007.xxxx
2009
- TUW-09-01 A. Rebhan, P. van Nieuwenhuizen and R. Wimmer, Quantum corrections to solitons and BPS saturation hep-th/0902.1904
- TUW-09-02 A. Rebhan, A. Schmitt and P. van Nieuwenhuizen, One-loop results for kink and domain wall profiles at zero and finite temperature hep-th/0903.5242
- TUW-09-03 D. Grumiller and P. van Nieuwenhuizen, Holographic counterterms from supersymmetry without boundary conditions hep-th/0908.3486
- TUW-09-04 M. Kreuzer, Heterotic (0,2) Gepner models and related geometries hep-ph/0903.nnnn
- TUW-09-05 M. Kreuzer, The making of Calabi-Yau spaces: Beyond toric hypersurfaces hep-ph/0903.nnnn
- TUW-09-06 P. M. Chesler, A. Gynther and A. Vuorinen, On the dispersion of fundamental particles in QCD and N=4 Super Yang-Mills theory hep-ph/0906.3052
- TUW-09-07 M.E. Carrington and A. Rebhan, On the imaginary part of the next-to-leading order static gluon self-energy in an anisotropic plasma hep-ph/0906.5200
- TUW-09-08 E. Avsar, E. Iancu, L. McLerran and D.N. Triantafyllopoulos, Shockwaves and deep inelastic scattering within the gauge/gravity duality hep-ph/0907.4604
- TUW-09-09 M. Schimpf and R.C. Rashkov, A note on strings in deformed AdS_4 x CP3 background hep-th/0908.2246
- TUW-09-10 H. Dimov, M. Michalcik and R.C. Rashkov, Strings in deformed T11: giant magnon and single spike solutions hep-th/0908.3065
- TUW-09-11 H. Dimov and R.C. Rashkov, On the pulsating strings in AdS_4 x CP3 hep-th/0908.2218
- TUW-09-12 D. Grumiller and A.M. Piso, Exact relativistic viscous fluid solutions in near horizon extremal Kerr background astro-ph.SR/0909.2041
- TUW-09-13 D. Grumiller and I. Sachs, AdS3/LCFT2 - Correlators in Cosmological Topologically Massive Gravity hep-th/0910.5241
- TUW-09-14 A. Gynther, A. Kurkela and A.Vuorinen, The N_f^3 g^6 term in the pressure of hot QCD hep-ph/0909.3521
- TUW-09-15 A. Rebhan, A. Schmitt and S. A. Stricker, Anomalies and the chiral magnetic effect in the Sakai-Sugimoto model hep-th/0909.4782
- TUW-09-16 S. Ertl, D. Grumiller and N. Johansson, Erratum to `Instability in cosmological topologically massive gravity at the chiral point' hep-th/0910.1706
- TUW-09-17 D.N. Blaschke, A. Rofner, R.I.P. Sedmik and M. Wohlgenannt, On Non-Commutative U_*(1) Gauge Models and Renormalizability - The BRSW model' hep-th/0912.2634
- TUW-09-18 D. Grumiller and O. Hohm, AdS3/LCFT2 - Correlators in New Massive Gravity hep-th/0911.4274
- TUW-09-19 A. Kurkela, P. Romatschke and A.Vuorinen, Cold quark matter hep-ph/0912.1856
- TUW-09-20 A. Rebhan and D. Steineder, Collective modes and instabilities in anisotropically expanding ultarelativistic plasmas hep-ph/0912.5383
- TUW-09-21 D.N. Blaschke, H. Grosse, E. Kronberger, M. Schweda and M. Wohlgenannt, Loop Calculations for the Non-Commutative U*(1) Gauge Field Model with Oscillator Term hep-th/0912.3642
- TUW-09-22 D. Grumiller and N. Johansson, Gravity duals for logarithmic conformal field theories hep-th/1001.0002
2008
- TUW-08-01 Ph. de Forcrand, A. Kurkela and A. Vuorinen, Center-Symmetric Effective Theory for High-Temperature SU(2) Yang-Mills Theory hep-ph/0801.1566
- TUW-08-02 V. Braun, M. Kreuzer, B. A. Ovrut and E. Scheidegger, Worldsheet Instantons and Torsion Curves, hep-th/0801.4154
- TUW-08-03 C. P. Herzog, S. A. Stricker and A. Vuorinen, Remarks on Heavy-Light Mesons from AdS/CFT, hep-th/0802.2956
- TUW-08-04 V. Batyrev and M. Kreuzer, Constructing new Calabi-Yau 3-folds and their mirrors via conifold transitions, math/0802.3376
- TUW-08-05 A. Rebhan, M. Strickland and M. Attems, Instabilities of an anisotropically expanding non-Abelian plasma: 1D+3V discretized hard-loop simulations hep-ph/0802.1714
- TUW-08-06 A. Fotopoulos and M. Tsulaia, Gauge Invariant Lagrangians for Free and Interacting Higher Spin Fields. A Review of the BRST formulation. hep-th/0805.1346
- TUW-08-07 M. G. Alford, M. Braby and A. Schmitt, Bulk viscosity in kaon-condensed color-flavor locked quark matter nucl-th/0806.0285
- TUW-08-08 E. Kiritsis, A. Schellekens and M. Tsulaia, Discriminating MSSM families in (free-field) Gepner orientifolds hep-th/0809.0083
- TUW-08-09 Changrim Ahn, P. Bozhilov and R.C. Rashkov, Neumann-Rosochatius integrable system for strings on AdS4 x CP3 hep-th/0807.3134
- TUW-08-10 R.C. Rashkov, A note on the reduction of the AdS4 x CP3 string model hep-th/0808.3057
- TUW-08-11 M. Kreuzer, R.C. Rashkov and M. Schimpf, Near Flat Space limit of strings on AdS4 x CP3 hep-th/0810.2008
- TUW-08-12 H. Dimov, R.C. Rashkov, Pulsating strings on AdS4 x CP3 hep-th/0811.xxxx
- TUW-08-13 H. Dimov, R.C. Rashkov, Multispin strings on AdS4 x CP3 I: giant magnon solutions hep-th/0811.xxxx
- TUW-08-14 M. Kreuzer, On the Statistics of Lattice Polytopes arXiv:0809.1188
- TUW-08-15 A. Rebhan, Nonabelian plasma instabilities in Bjorken expansion hep-ph/0810.2805
- TUW-08-16 A.M. Kasprzyk, M. Kreuzer, B. Nill, On the combinatorial classification of toric log del Pezzo surfaces arXiv:0810.2207
- TUW-08-17 A. Rebhan, Hard loop effective theory of the (anisotropic) quark gluon plasma hep-ph/0811.0457
- TUW-08-18 M.E. Carrington and A. Rebhan, Next-to-leading order static gluon self-energy for anisotropic plasmas hep-ph/0810.4799
- TUW-08-19 A. Rebhan, A. Schmitt and S. A. Stricker, Meson supercurrents and the Meissner effect in the Sakai-Sugimoto model hep-th/0811.3533
- TUW-08-20 A. Collinucci, M. Kreuzer, C. Mayrhofer and N.-O. Walliser, Four-modulus "Swiss Cheese" chiral models hep-th/0811.4599
- TUW-08-21 R.S. Garavuso, M. Kreuzer and A. Noll, Fano hypersurfaces and Calabi-Yau supermanifolds hep-th/0812.0097
- TUW-08-22 A. Collinucci, New F-theory lifts hep-th/0812.0175
- TUW-08-23 S. Beane, D.B. Kaplan and A. Vuorinen, Perturbative nuclear physics nucl-th/0812.3938
- TUW-08-24 A. Vuorinen, Equation of state of zero-temperature quark matter with finite quark masses hep-ph/0810.3595
Previous years
For published articles, talks, and poster presentations see Publications
